この記事は、心理系大学院生を対象とした統計法の学習ページです。
- AICってなに?
- モデル選択基準について勉強したけどよくわからない
- 重回帰分析で複数のモデルを比較する方法を知りたい
こんな悩みや疑問がある方はご参考ください( ˘ω˘)
赤池情報量基準とは?
赤池情報量基準とは、別名AICと言われ、重回帰式(モデル)の当てはまり度を表す統計量のことをいう。
当てはまり具合と言われると、決定係数と何が違うの?
と思うかもしれませんが、次のような違いがあります。
- 決定係数・・・重回帰式単体のデータの予測に対する当てはまりの良さ
- AIC・・・他の当てはまりのモデルと比較した際の良さ
つまり、重回帰式が、A・B・Cと3つある時、どの式が最も母集団のデータを正確に予測しているかを示すための指標のことなのです!
研究でAICを使う場面
多くの場合、研究で重回帰分析を行う時というのは、1つだけのモデルを研究することは、珍しいと思われます。
例えば、従属変数を固定して、独立変数AとBの組み合わせ、AとC、BとCの組み合わせといった様にモデルを複数検証する。
あるいは、先行研究で言われていることが自分が集めたデータにも当てはまるのかを確認するために、重回帰分析を行うなどする。
これらの様なケースでは、前者であれば、自分の研究内でのモデルにおいてどれが最良のモデルかを検討する意味があるし、後者であれば先行研究のモデルと比較する意味がある。
この様な時に指標となるのがAICというわけ。
「複数の重回帰式から、最良の重回帰式を選択しなければならないことがあります。
①説明変数を変えて重回帰分析を多数回行ったとき、どの重回帰式がよいか
②他の研究で行われた重回帰分析の結果と比較したとき、どちらの重回帰式が良いか」
(引用:例題とExcel演習で学ぶ多変量解析 P112, 1-3行目)
具体的に…
では、例のごとく、↓↓この出力結果を使ってAICを求めていきましょう(^ω^)
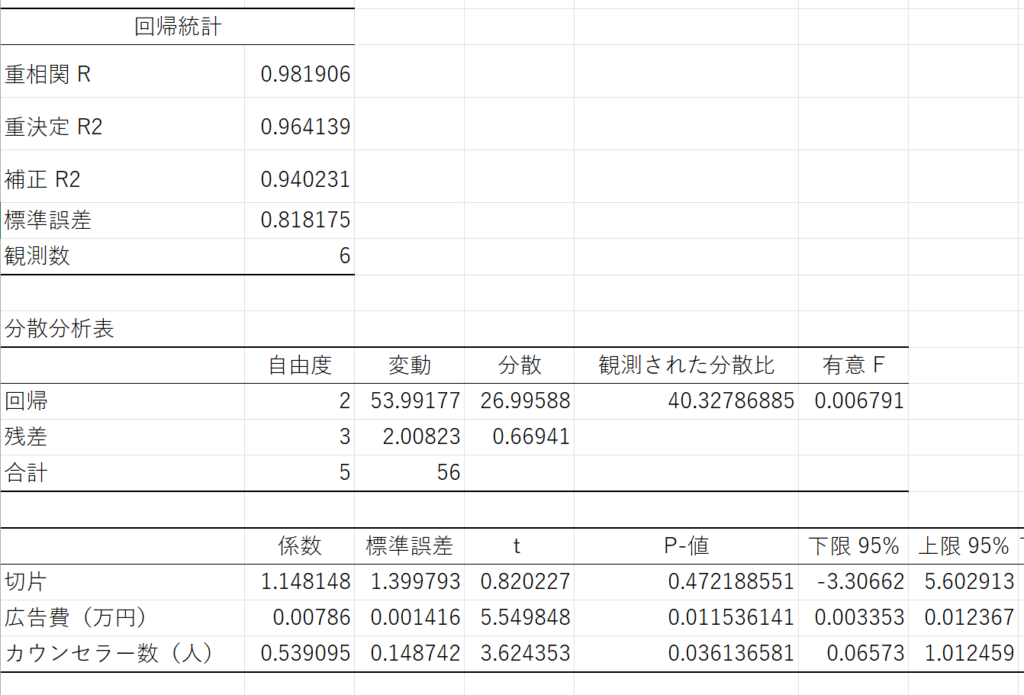
係数の確認をすると、以下の通りですね。
- 切片:1.148148
- 広告費:0.00786
- カウンセラー数:0.539095
AICを求める際は、以下の公式を使います。
- AIC = n(log(Se/n) + log(2π) + 1) + 2(p + 2)
※ n = サンプル数、Se = 残差平方和、p = 説明変数の数、logは自然対数
これを計算すると、18.46となります!
やってみましょう。
- n(サンプル数/観測数) = 6
- Se(残差平方和) = 2.00823
- p(説明変数の数) = 2(広告費とカウンセラー数)
これらを先ほどの公式に代入して計算すると↓↓こうなります!
①AIC = 6 × (log(2.00823/6) + log(2π) + 1) + 2(2 + 2)
②= 6 × (log(0.334705) + log(6.283185) + 1) + 8
③= 6 × (-1.094537 + 1.837877 + 1) + 8
④= 6 × 1.74334 + 8 = 10.46004 + 8 = 18.46
ですが!
こんな計算のプロセスは、わからなくていいです(笑)
なぜかって?
実際は、統計ソフトがやってくれるからです(笑)
AICの活用の仕方について
そして、問題は、この「18.46」といった値をどの様に活用するのか!?ということです
「重回帰式の選択は、次に示すモデル選択基準と呼ばれるAIC、CAIC、Cp、MCp、Peを適用します。モデル選択基準AICは予測の観点から、よいモデルを求める基準です。CAICは上記①、その他のモデル選択基準は②の場面で適用されます。モデルの選択基準はどの方法も、値が小さいがよいモデルといえます。」
(引用:例題とExcel演習で学ぶ多変量解析 P112, 4-8行目)
つまり、このモデルにおけるAIC = 18.46となったが、モデルがA~Cの3つがあり、以下の様な結果になったとしたら、
- モデルA → 18.46
- モデルB → 20.21
- モデルC → 16.93
「モデルC」が、母集団を説明する上で、最適だと判断することができるわけですね~
ちなみに、AICはパス解析など他の大変量解析においても用いられる指標なので覚えておきましょう(=゚ω゚)ノ
まとめ
いかがでしたでしょうか?
AICについて少しは理解が深まったでしょうか?
最後に本記事の内容を振り返っておわかれです(^^)/
- AICとは、赤池の情報量基準のことで、複数のモデルを比較した際の当てはまりの良さを示す指標
- 決定係数とAICの違いは、決定係数は母集団に対する当てはまり、AICは他のモデルと比較した際の良さを示す
- AICの値は、小さいほど良いモデルと判断できる
ということなんですね~
それではまた(^^ゞ
こちらの内容を動画で学びたい方は
※ページの最下部からこの記事の感想をコメントしてください。その後、パスワードをお送りします(^^ゞ
参考
こちらの記事を作成にする上での参考文献です(^ω^)
①多変量解析がわかる
②多変量データ解析法
③例題とExcel演習で学ぶ多変量解析






コメント