【特徴②】回帰直線はデータとの〇〇が最小になるように引く線です～わかりやすく解説～

この記事は、この記事は、修士論文のサポートを目的として、臨床心理士指定大学院生向けです。

こんな方はぜひご覧ください(^^ゞ

それでは本編です。

ちなみに、今回は、回帰直線の特徴についてまとめてます。

結論～実測値と予測値のずれが最小となるように引かれる線～

前回までのおさらいをすると

ということでした。

そして、今回のポイントは、回帰直線が

「実際のデータと回帰直線による予測値とのズレが、最も小さくなる様に引かれる線」であるということです。

例えば

↓↓こんな散布図があったとしたら

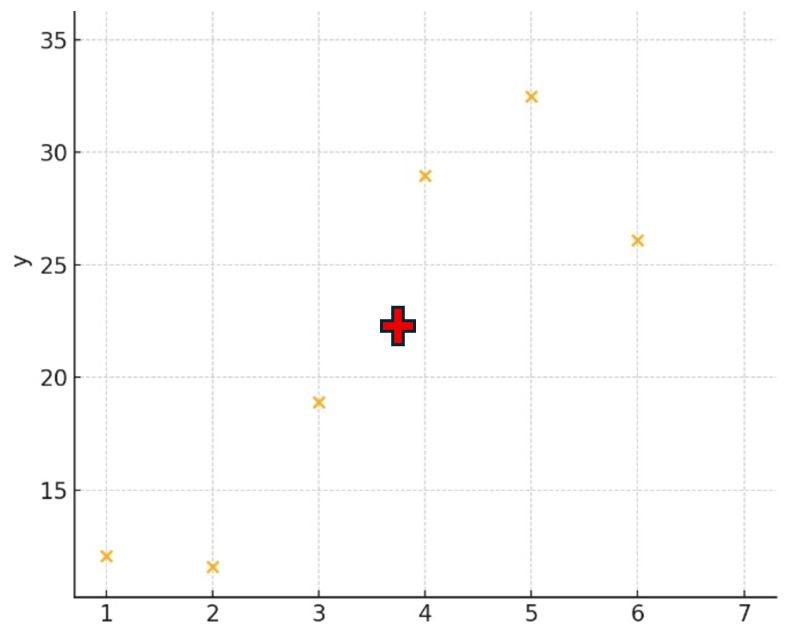
回帰直線は、「×」マークを通るように引かれる線のことでした。

「×マーク＝変数ｘとｙの平均値」です。

しかしながら、この平均値を通る線なら、なんでもいいのかというとそうではありません。

なぜなら、その条件だけであれば、以下のように色んなパターンが考えられます。

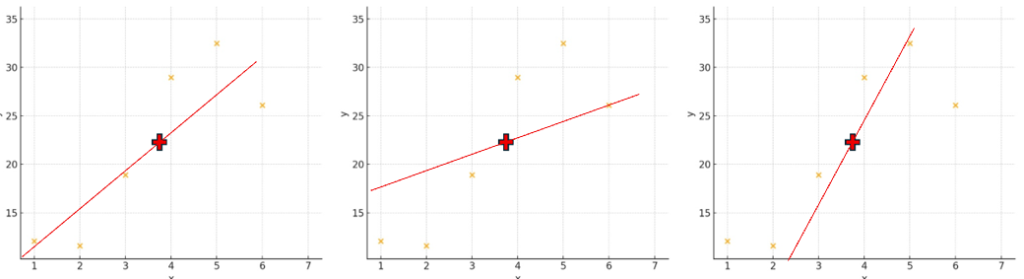
そこで、「回帰直線＝２つの変数の平均を通る」という条件に加えて、

「データ個々とのズレが最も小さくなるような線」というもう１つの条件が加わります。

ただ、データ個々とのズレと言われても、よくわからないと思うので、具体的にみてみることにします。

例えば、先ほどの散布図において、x＝4の時のデータをみてみることにします

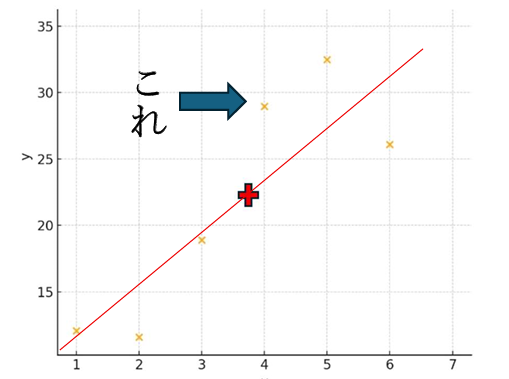
そして、このデータと回帰直線とのズレというのは・・・

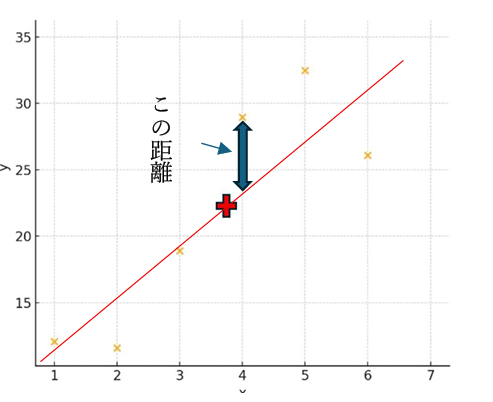
このようなデータと回帰直線との距離のことを意味してます

これで、「データと回帰直線とのズレ」が何を言っているかわかりました。
では、このずれが大きいとか、小さいとかいうのはどういうことでしょうか？

まず、「ズレが大きい」というのは↓↓こういうことです

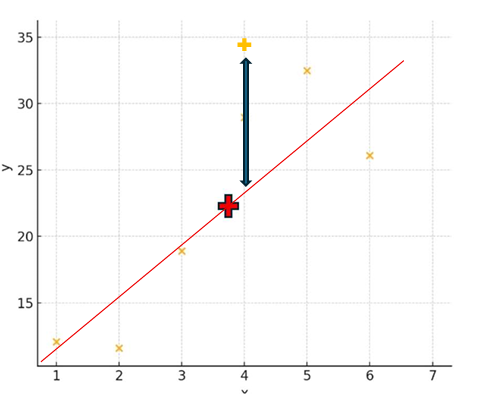
先ほどと比べて、データと回帰直線の距離が⾧くなってますね。
逆に小さいというのは、↓↓こういうことですね。

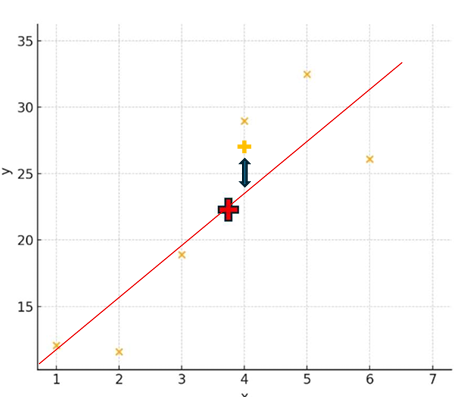
データと回帰直線の距離が短くなってますよね？
つまり、この様にズレを小さくするというのは、実測値と予測値の誤差が小さいというこ
とを意味するわけです。

ただし、ここでの「ズレ」はx＝4の場合だけの話をしてるので、他のデータも含めて、
「データ全体とのズレを小さくする」という話になります

↓↓これらの距離の合計が最も小さくなるように引く線

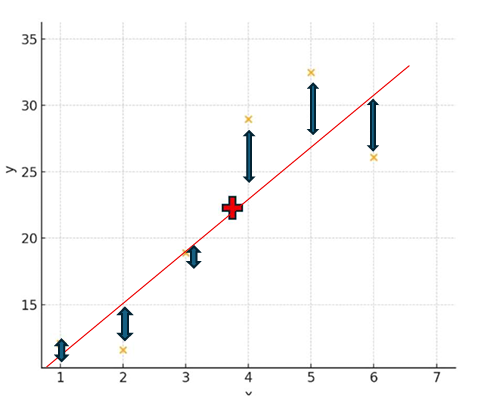
だから、「個々のデータと回帰直線とのズレが最も小さくなる様な線＝回帰直線」ということなんですね。
そして、この「個々のデータと回帰直線とのズレが最も小さくなる様な線」を求める方法
を「最小二乗法」といいます。
最小二乗法について詳しく知りたい方は↓↓こちら（＾＾）

それでは、最後に本記事の内容をおさらいしておわかれです。

ということでしたね～
それではまた(^^ゞ

工事中