こちらは、心理系大学院生向けの記事まとめです(^^♪
- パス図ってなに?
- どうやって書けばいいの?
- 図の読み取りや見方が知りたい!
こんな疑問がある方は、ぜひご参考ください。
結論~パス図とは~
結論から言うと、パス図とは、変量の関係を可視化した図です。
具体的には、「y=ax+b」の回帰式をパスで表したものが
↓↓こちら
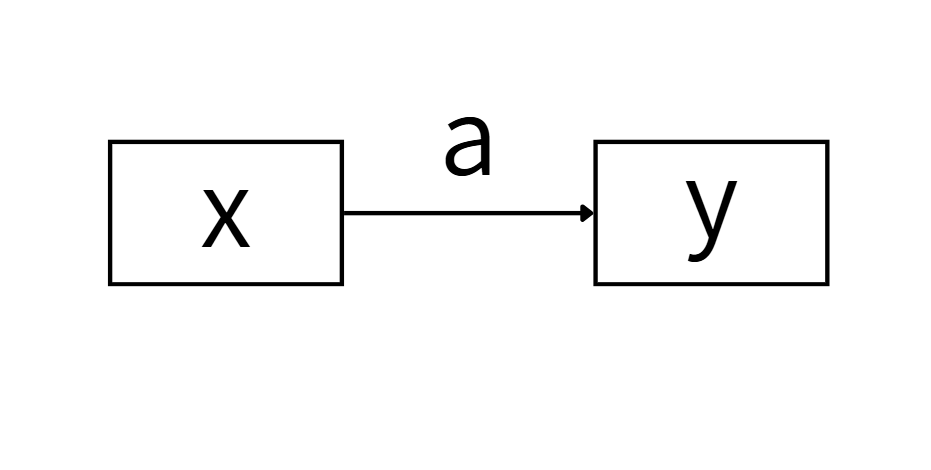
これは、変量xが、変量yに影響があることを示しています。
そして、「a」というのはその影響力の大きさを示しています。
つまり、「a=回帰係数」ということになります。
ただし、パス図は、分析手法によって書き方が異なるので、aの意味も分析手法によって異なる点には注意が必要です。
具体例
さて、とはいっても、具体的な数値がないとわかりづらいと思うので、
仮に、以下のような変数があったとします。
- 変数x・・・勉強時間
- 変数y・・・テストの点数
そして、これらのデータに基づいて、回帰分析を行った結果
- y=0.5x+8
といった式が得られたとします。
この式をパス図で表すと
↓↓こうなります
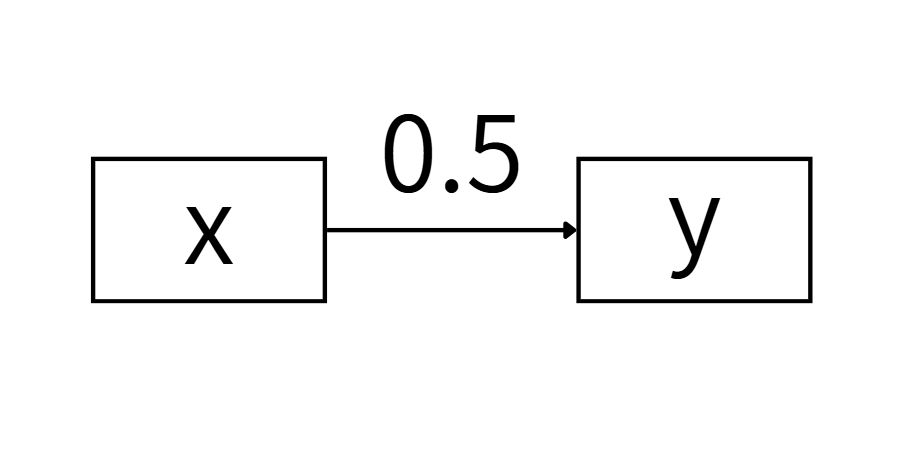
「パス図では、資料に現れる変量(観測変量といいます)は四角枠で囲みます。そして「影響を与える」という関係は一方向矢印(パスといいます)で表します」
(引用:多変量解析がわかる,p31,1-3行目)
つまり、変量x(勉強時間)は、変量y(テストの点数)に「0.5」だけ影響を与えているということになります。
回帰式だけでは説明できない部分(誤差)も示す
ただし、過去記事でも触れてきたように、回帰式はあくまで「予測式」です。
つまり、100%正確な値を導くわけではありません。
ということは、パス図には「その誤差」も示しておくほうが親切ですね。
それを示したものが↓↓こちらです
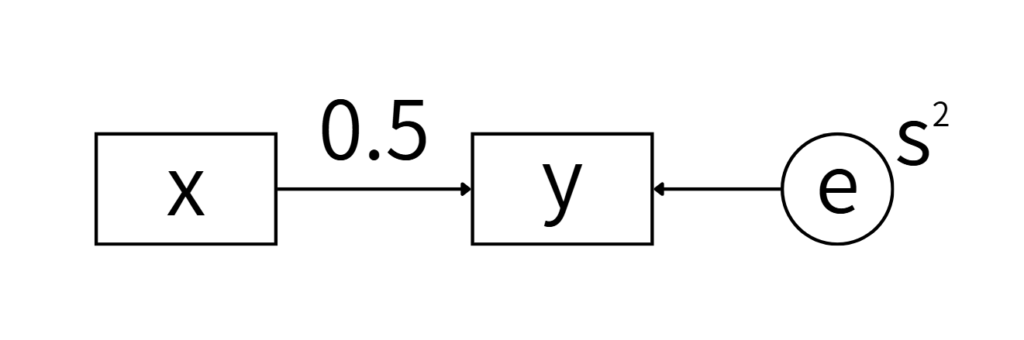
「その誤差を表す変量、すなわち誤差変数は円で表します。そして、その誤差変数の分散s2は誤差変数の分散を表しているのです。一般的に、変量xがyに影響し、そのxで取りこぼした誤差を誤差変数eで表したのが下図です。」
(引用:多変量解析がわかる,p31,2段落,3-7行目)
繰り返しになりますが、パス図の書き方や意味は分析手法によって異なるので、この記事ではあくまで回帰分析の文脈によるものです。
まとめ
さて、いかがでしたでしょうか?
パス図についての理解が少しは深まったでしょうか?
最後に、本記事の内容を振り返ってお別れです(^^)/
- パス図とは、変量の関係を可視化した図です。
- パス図における「a」は「回帰係数」を表している。ただし、分析手法によって意味が異なる。
- パス図では、観測変量をは四角枠で囲んで表す。ある変数から別の変数への影響を「→」で表し、これを「パス」と呼ぶ。
- 回帰式で取りこぼした部分は、「誤差」としてパス図に示す必要がある。誤差は「e」で表し、誤差変数の分散でもある。
- パス図の書き方は分析手法によって異なる。
ということなんですね~
それではまた(^^ゞ
参考書
最後に、本記事を作成する上での参考文献を紹介します(^^♪
①多変量解析がわかる
②図解雑学 多変量解析





コメント