【特徴①】回帰直線とはどんな線？～わかりやすく解説～

この記事は、修士論文のサポートを目的として、臨床心理士指定大学院生向けです。

• 回帰分析についてのレポートがある
• 研究で回帰分析を行うので理解を深めたい

こんな方はぜひご覧ください(^^ゞ

それでは本編です。

ちなみに、今回は、回帰直線の特徴についてまとめてます。

結論～回帰直線ってどんな線？～

結論からいうと、回帰直線は2つの変数の平均値を通る直線だと言われています。

仮に、こんな散布図があったとしたら

回帰直線は、この辺の点を通るということです。

ひとまず、このことだけ理解しておけばOKです。

なぜなら、この特徴を理解しておくことは、回帰直線を求める上で知っておくべき内容だからです。

修士論文を進める上ではわかってなくても大丈夫です。

なぜなら、SPSSがやってくれるから。

とはいえ、実際に分析をする上ではわかっておきたいところでもあります。

そのため、回帰分析についての理解を深めたいという方は読み進めてみてください(^^♪

もう少し具体的な話

では、ここから回帰直線は2つの変数の平均値を通る直線であるという点をもう少し具体的にしていきます。

まず、あなたに思いだしてもらいたいのは

回帰直線は式で表すとどんな線だったでしょうか？

ということです

そうですね。

• y = ax + b

のような形式でした。

そして、この直線を求める際のポイントが

「説明変数xと目的変数yの平均を通る線」

だということです。

なぜなら、回帰直線というのは、散らばっているデータの真ん中を通る線だからです。

さきほどの、散布図に今度は回帰直線をひいてみましょう。

すると、以下の様なイメージになります。

「真ん中」という表現は、必ずしも適切ではありませんが、ここで大事なのは、イメージです。

「回帰直線＝散らばったデータの真ん中を通る線」

というイメージなんです。

なぜか？

「真ん中」に線を引くということは、

真ん中の代表とも言える値

つまり、「平均値」を通るということだからです。

では、何の平均値？

と言われたら、もちろん

変数xと変数yの平均値です。

実際にやってみましょう

仮に以下の様なデータがあったとします。

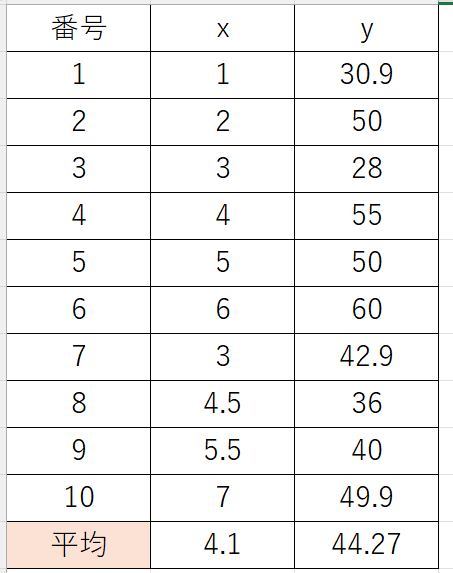
このデータの場合、xの平均値が「4.1」で、yの平均値が「44.27」でした。

そのため、以下のように✖️マークのあたりがその位置になります。

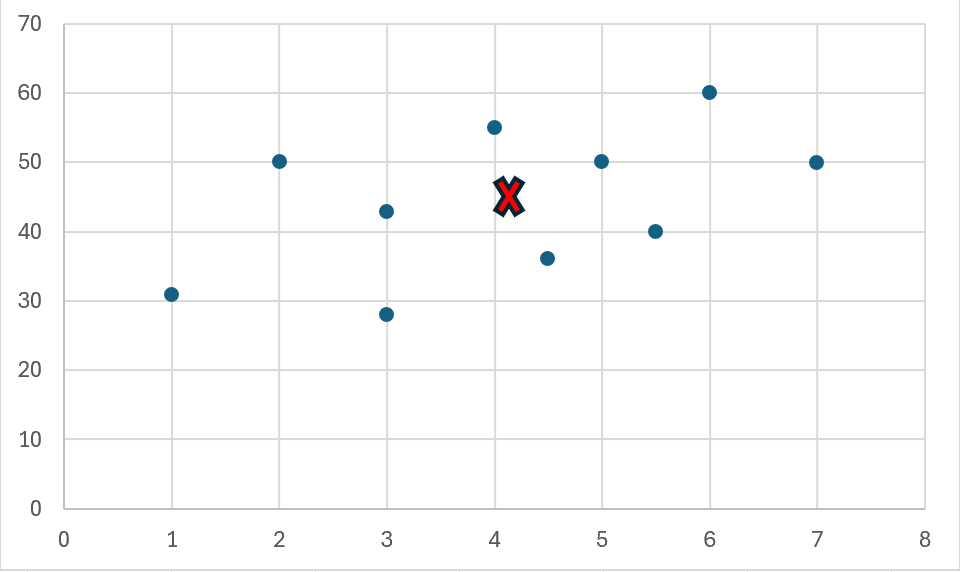
そして、ここに引かれる回帰直線というのは、以下の特徴を持つ直線ということになります。

1. 傾き= a
2. 切片= b
3. xとyの平均値を通る

ちなみに、

• y = ax + b

が成立するとき、aとbについて以下の公式が成立します。

1. a = Sxy / Sx2 (xとyの共分散÷xの分散）
2. y_＝b+ax_

※y_=yの平均、x_=xの平均

ただ、成り立つけど、覚える必要はありません。

「そういう、公式があるんだよ」

と思ってればOKです。

「じゃぁ、何で、この話するんだよ」

と思うかもしれませんが、ここから、回帰直線

y = ax + b

がxとyの平均を通る線であることを証明するためですね。

回帰直線がxとyの平均値を通る線であることの証明

なぜ、覚えなくていい公式の説明をしたうのか？

それは、

「y = ax + b」は「y_=a(x-x_+y_）」と書き換えることができるからです。

数式アレルギーがある方はもはや

「は？」

というレベルかと思いますが、ここで言ってるのは

「りんご　＝　赤いくだもの」

のように、表現の仕方をただ変えてるだけで、本質的には同じものなんですよとイメージしてください（笑）

そして、この書き換えた式が、xとyの平均を通る線であることを証明してくれます。

公式を変形してみる

実際にやってみましょう

まず、「2」の公式を

「b ＝ y_-ax_」に変形します。

次に、これを「y = ax + b」に代入します。

すると、「y = ax + y_-ax_」になります。

これをa でくくると

y_=a(x-x_+y_）

　になります。

なので、

「y = ax + b」は「y_=a(x-x_+y_）」

になるんですよ、というのがここでのポイントですね。

「y_=a(x-x_+y_）」は平均を通る線

では、この線が２つの変数の平均点を通ることを証明するにはどうすればいいでしょうか？

それは実際にデータの値を代入することです。

先ほどのデータでは、

• x_ = 4.1
• y_ = 44.27

でした。

これを代入すると

y_=a(x- 4.1） + 44.27

となります。

であれば、この式に

x = 4.1 を代入して、yの値が44.27になればいいというわけです。

すると

y = a（4.1 – 4.1） + 43.27

なので、まず　（　）内を計算し

「4.1-4.1＝0」ですね？

aの値が分からなくても、a×0 =0にしかなりません。

従って

y = 0 + 44.27 = 44.27

ということです。

これで、

「y_=a(x-x_+y_）」は「x=4.1」のとき「y=43.27」を通る線であることが証明されました(^^♪

で「y_=a(x-x_+y_）」はy = ax + b をただ書き換えただけなので、

すなわち、y = ax + b も平均を通る線であることが証明されましたね〜

まとめ

それでは、最後に本日の記事をさらってお別れです。

• 回帰直線は、データの散らばりの「真ん中」に引かれた直線のこと
• 回帰直線は、変数xと変数yの「真ん中」におる平均値を通る直線だと言える
• 「y = ax + b」は「y_=a(x-x_+y_）」と書き換えることができる

ということなんですね～

それではまた(^^ゞ

参考

この記事を書く上で参考にした書籍をのこしておきます

①図解雑学 多変量解析

②多変量解析がわかる