この記事は、心理系大学院生を対象とした統計法の学習ページです。
- 重回帰モデルとパス図ってなに?
- 重回帰分析について勉強したけど、モデルとパス図の関係がよくわからない
- ついでに、書き方もわからない
こんな悩みや疑問がある方はご参考ください( ˘ω˘)
重回帰分析における、モデルとパス図とは?
結論から言うと、
- 重回帰モデル = 式
- パス図 = 式を図にしたもの
という様なイメージを持っておくと良い。
では、片方ずつみていくことにしましょう(^ω^)
重回帰モデルとは
まず、重回帰モデルというのは具体的に↓↓これ
- 売上 = a×広告費 + b×人員数 + c
このような式のことを言います。
「重回帰分析の基本式として、重回帰モデルと呼ぶ」
(引用:多変量データ解析法、P37. 4-5行目)
パス図とは
そして、このモデルを可視化したのがパス図となるわけです。
先程の重回帰モデルをパス図にしたのが↓↓これ
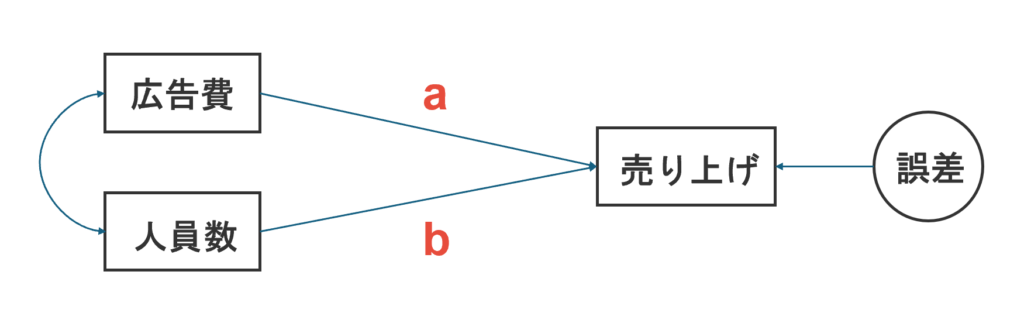
重回帰モデルは、図4.1(A)のパス図を用いて視覚的に表わされる。パス図では、観測される変数は四角で、誤差を円で描く
(引用:多変量データ解析法 P37.6-7行)
パス図の見方
そして、広告費から売り上げに伸びる矢印に「a」、人員数から売り上げにのびる矢印に「b」と記載がありますが、これは、回帰係数をあらわしています。
パスに添えられたb1. b2. b3. が説明変数に乗じられ、これらと切片cの和が予測値になることを表している
(引用:多変量データ解析法、P37. 8-9行)
補足として、独立変数間にある両矢印は、相関を示している。
なお、図の左に描かれた説明変数間の両矢印は相関係数を表すものである
(引用:多変量データ解析法、P37.11-12行)
まとめ
さて、いかがでしたでしょうか?
重回帰モデルとパス図について少しは理解が深まったでしょうか?
最後に本記事の内容を振り返っておわかれです(^^)/
- 重回帰モデルとは、「売上 = a×広告費 + b×人員数 + c」のような式のこと
- パス図とは、重回帰モデルを視覚的に表したもの
- パス図では、観測される変数は四角で、誤差を円で描く
- 矢印に添えられたアルファベットは回帰係数をあらわす
- 独立変数間の両矢印は、相関係数を表す
ということなんですね~
それではまた(^^ゞ
こちらの内容を動画で学びたい方は
※ページの最下部からこの記事の感想をコメントしてください。その後、パスワードをお送りします(^^ゞ
参考
こちらの記事を作成にする上での参考文献です(^ω^)
①多変量解析がわかる
②多変量データ解析法
③例題とExcel演習で学ぶ多変量解析






コメント