回帰直線とは、「個々のデータとのズレ、つまり、「残差」をすべてたし合わせたときな最小になるときの直線」でした。
つまり、以下の赤矢印で示したのがズレなので、これらを全部足し合わせた値が最小になるように引く線が回帰直線ということですね。

しかし、このまま足すと、「マイナス」の値があるので、全て二乗にして、値をプラスに足し合わせるというのが「最小二乗法」の考え方でした。
つまり、最小二乗法というのは「予測値と実測値のズレを小さくしましょう」ということです。
ここまでは、これまでの記事内容でも触れてきましたが、今度はこの話を「分散」といった視点から捉えてみたいと思います。
ズレを小さくする=誤差の分散を小さくする
なぜ、「分散といった視点」を取り上げるのかというと、多変量解析の主役は分散だからです。
では、分散とはなんだったでしょうか?
それは、「データのばらつき」を意味していました。
つまり、「予測値と実測値のズレを小さくしましょう」という表現は
「予測値と実測値のズレの分散(ばらつき)を小さくしましょう」ということでもあります。
さらに統計的用語を使って言い換えるのであれば
「回帰直線=残差の分散を最小にする」ということになります。
↓こうではなく
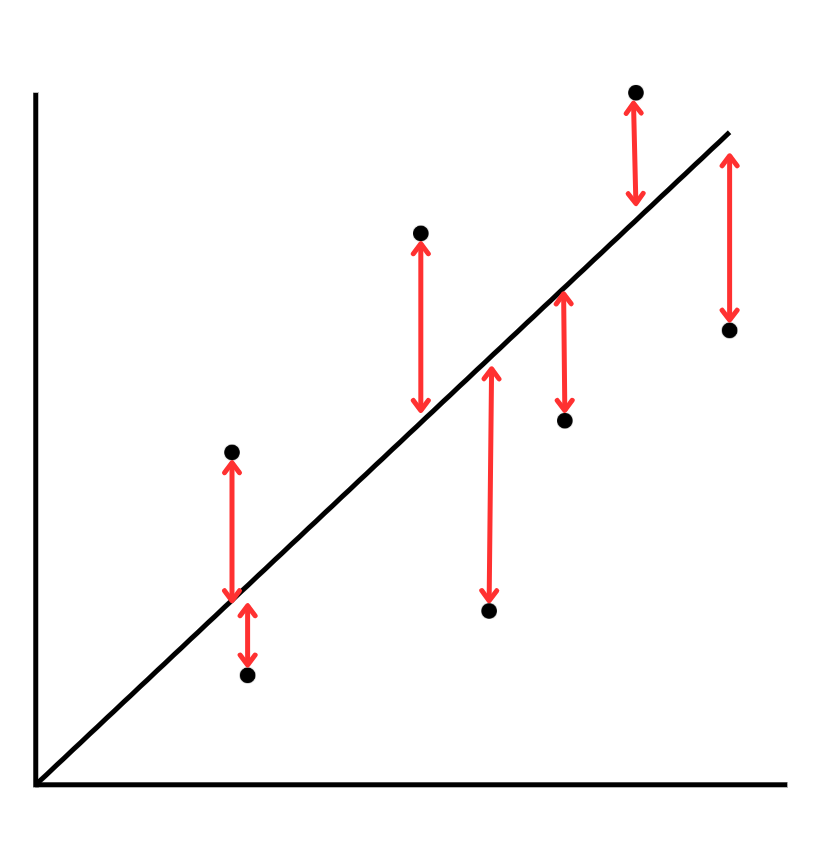
↓こうがいいよね
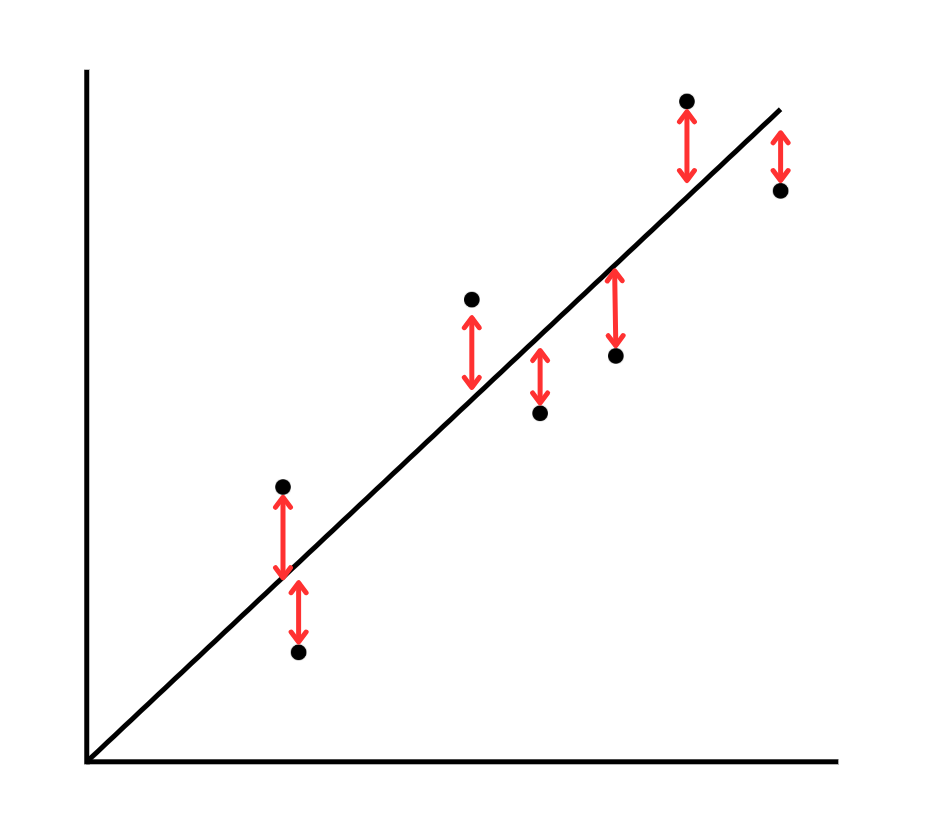
という話です。
なぜなら、分散(ばらつき)が小さいからです。
そして、「分散(ばらつき)が小さい=精度の高い回帰直線」だからです。
分散について詳しく理解したい方は↓↓こちら(=゚ω゚)ノ
実測値の分散=予測値の分散+誤差の分散
ここまでの話を見える可すると↓↓このようになります。
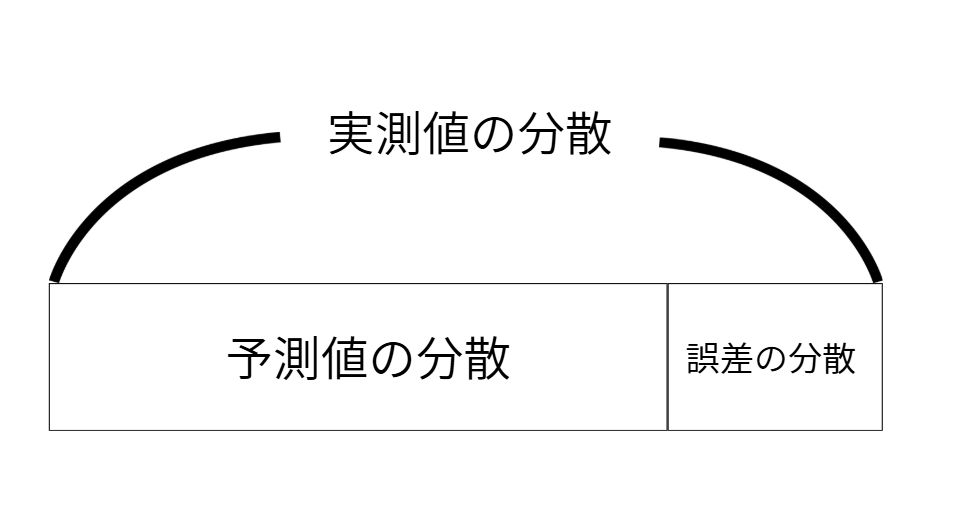
なので、誤差の分散を小さくするというのは・・・
↓↓こういうことです
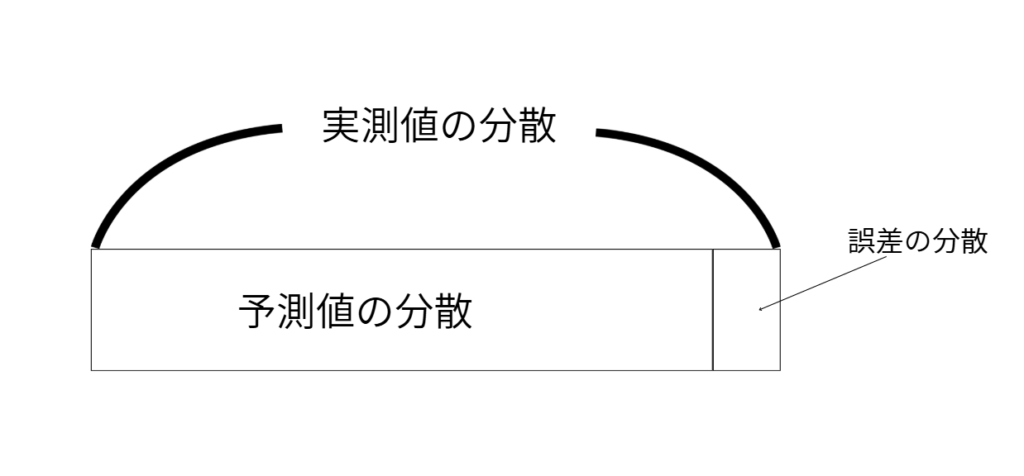
そして、誤差の分散を小さくするということは、すなわち
「説明変量の分散を最大化すること」と同義なわけですね!
だから、回帰分析では、「残差の分散を最小すること」を目指すわけです
まとめ
最後に本記事の内容を振り返っておわかれです(^^)/
- 予測値と実測値のズレを最小にすることは、残差の分散を最小にすること
- 「目的変量の分散=説明変量の分散+残差の分散」で表すことができる
- つまり、「残差の分散を小さくする=説明変量の分散を小さくする」こと
ということなんでね~
それではまた(^^ゞ
参考書
最後に、本記事を作成する上での参考文献を紹介します(^^♪
①多変量解析がわかる
②図解雑学 多変量解析






コメント