この記事は、心理系大学院生を対象とした統計法の学習ページです。
- 残差と誤差ってどう違うの?
- 重回帰分析について勉強したけど、残差と誤差の違いがよくわからない
こんな悩みや疑問がある方はご参考ください( ˘ω˘)
結論
結論から言うと、この2つは具体性に違いがあります。
残差は、固有値であり、これ以上なく具体的な値です。
一方、誤差は、モデルとしてのズレがあることを示す表現です。
とはいえ、この説明だけではよくわからないこともあると思うので、それぞれを確認していきます。
残差とは
残差とは、「個々のデータごとの従属変数値の実測値と、予測値の具体的な差」のことを言います。
「この137-127=10のように、誤差の具体的数値のことを残差と呼ぶ」
(引用:多変量データ解析法、P39.9行目)
例えば、これまでの題材として扱ってきた↓このデータ
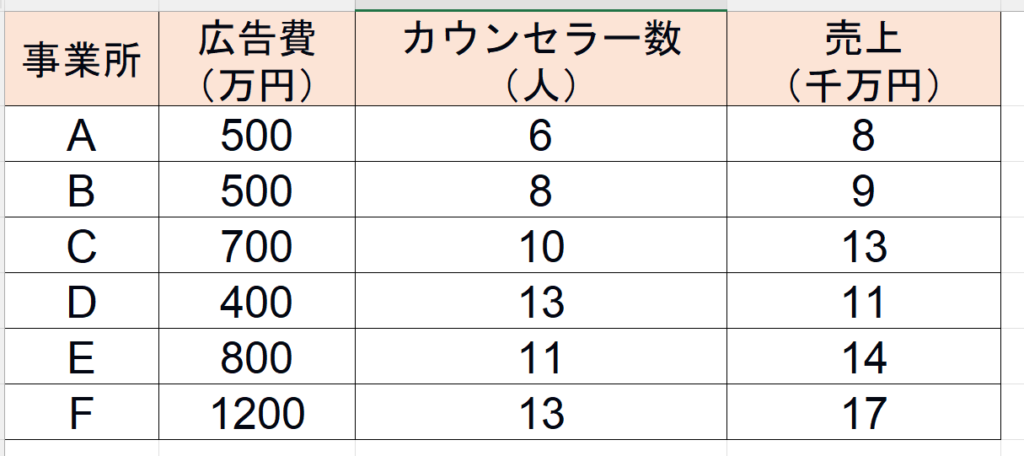
- 広告費・・・独立変数①(x)
- カウンセラー数・・・独立変数②(z)
- 売上・・・従属変数(y)
そして、このデータに基づいて求められた重回帰式が↓これ
- y = 0.008x + 0.539z + 1.148
でした。
※この辺式の詳しい求め方が知りたい方はこちら
そして、この式は「予測式」です。
つまり、当たることもあれば、当たらないこともあります。
↓こういうことです
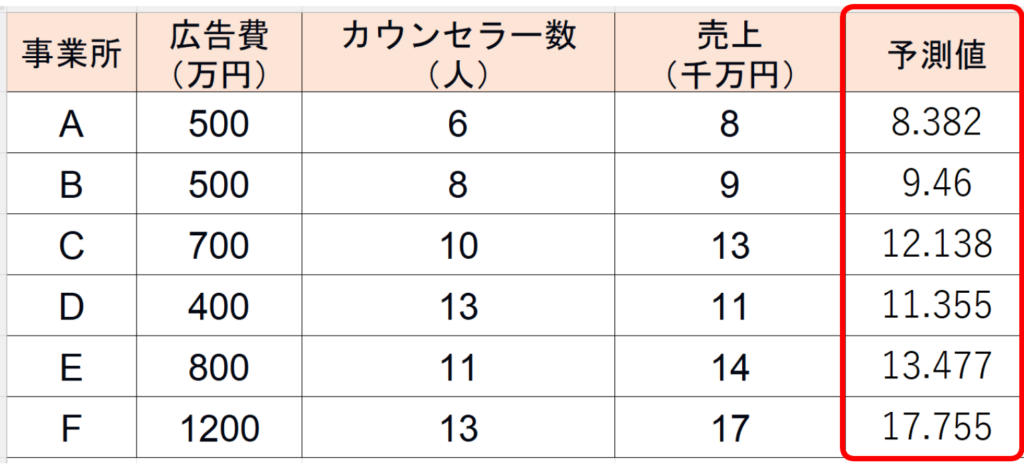
これは先程のデータに5列目を増やし、先程の重回帰式にデータの値を代入して具体的な値を求めた表です。
これをみてわかる様に、実測値より小さいこともあれば、大きいこともあるし、一致することもあります。
なぜなら予測値だからです。
残差の計算例
そして、残差とは「データごとの従属変数の実測値と、予測値の具体的な差」のことでした。
ここでの従属変数は「売上額」でしたから、事業所Aの場合・・・
- 実測値 = 8
- 予測値 = 8.382
ということですね!
「実測値-予測値=差」なので
- 8 – 8.382 = -0.382
となります。
つまり、「-0.382」がデータAの残差となります。
この計算を全てやると↓こうなります
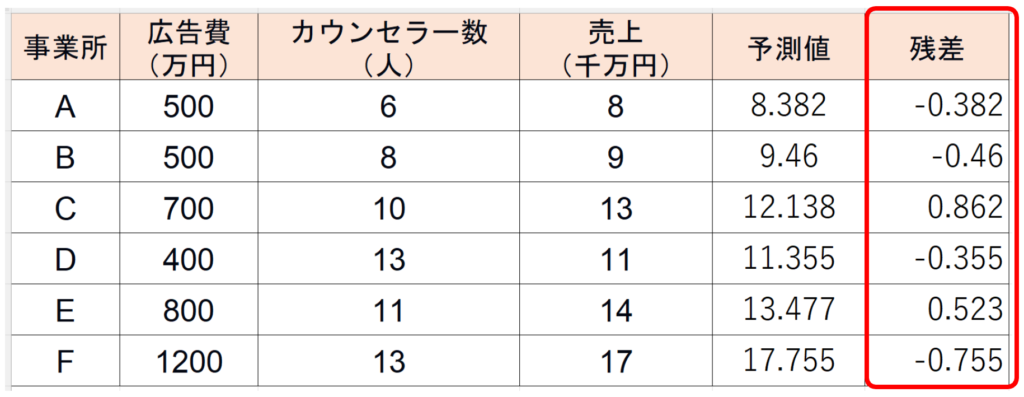
これらの「具体的な値=残差」というわけです。
誤差とは
一方、誤差とは、「重回帰式では説明しきれない部分」という意味で、モデルとして、あるいは、理論的な説明の際に使う表現です。
つまり、残差に比べると「抽象的」になります。
「誤差=「説明変数では説明しきれずに残った成分」(4.6)」
(引用:多変量データ解析法、P37.下から3行目)
この辺を詳しく理解したい方は↓↓こちら
一応、イメージとしてまとめておくと赤枠で囲った部分が誤差です
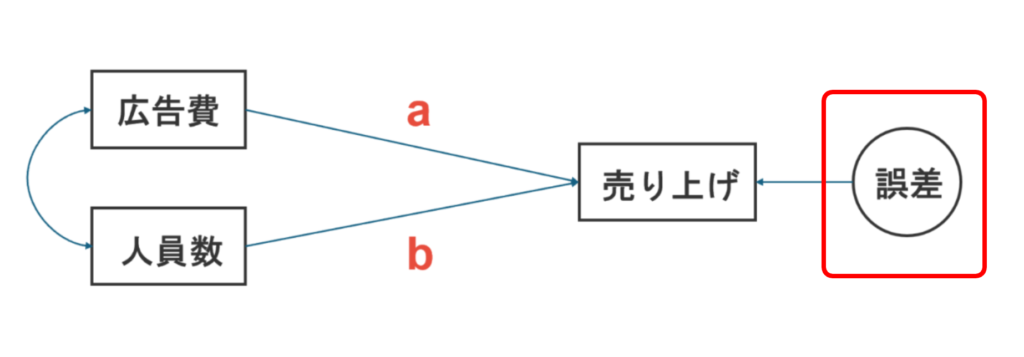
「すなわち、(4.3)-(4.5)式のようなモデルに現れる従属変数と予測値の差を「誤差」と呼ぶのに対して、分析後に求められる誤差の具体的な値を「残差」と呼ぶ」
(引用:多変量データ解析法、P39.9-11行目)
誤差の具体的な意味
ただ、ここで、もう少しだけ「モデルに現れる」の部分を具体的に考えると、
「モデル」とは、「重回帰式」のことでした。
つまり、↓これです
y = 0.008x + 0.539z + 1.148
そして、「誤差」とは、「説明変数では、説明しきれずに残った部分」なので、
事業所Aでいえば
8 – (0.008x + 0.539z + 1.148)
と表わすことができます。
これが、「誤差」です。
ただ、これだと具体的数値がわかりませんよね?
あくまで「構造式的な説明」ということになります。
これが、誤差は「モデルとしてのズレがあることを示す表現」ということの意味です。
事業所A~Fまでの誤差を示すと↓こうなる
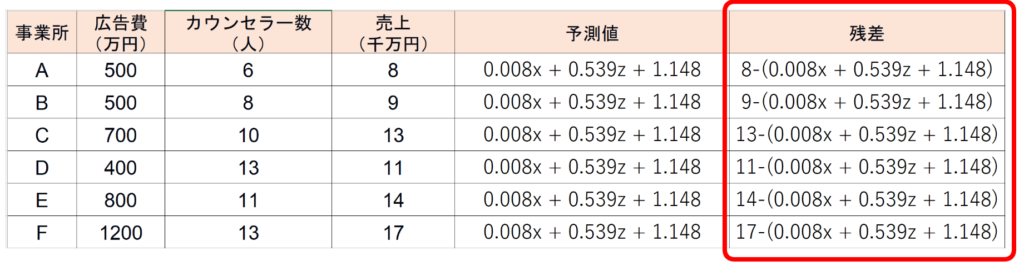
計算のやり方としては、残差の時と同じです。
違うのは、実測値から、具体的な予測値を引くのか、それとも、予測式を引くのか、それだけです。
まとめ
いかがでしたでしょうか?
残差と誤差の違いについて少しは理解が深まったでしょうか?
最後に本記事の内容を振り返っておわかれです(^^)/
- 残差と誤差は具体性が異なる。
- 残差とは、個々のデータごとの実測値と予測値の具体的な差のこと
- 誤差とは、モデルとしてのズレを示す抽象的な表現のこと
- 残差は具体的な数値、誤差は構造式として使われる
ということなんですね~
それではまた(^^ゞ
こちらの内容を動画で学びたい方は
※ページの最下部からこの記事の感想をコメントしてください。その後、パスワードをお送りします(^^ゞ
参考
こちらの記事を作成にする上での参考文献です(^ω^)
①多変量解析がわかる
②多変量データ解析法
③例題とExcel演習で学ぶ多変量解析







コメント