この記事は、主に臨床心理士指定大学院生にむけた統計法学習シリーズです(^^♪
- 回曲線ってどんな直線?
- 回帰曲線の式はどうなる?
こんな疑問がある方は、ぜひご参考ください!(^^)!
結論~回帰曲線とは~
まずは結論からいきましょう。
回帰曲線とは、↓↓このような回帰線を描くものを言います。
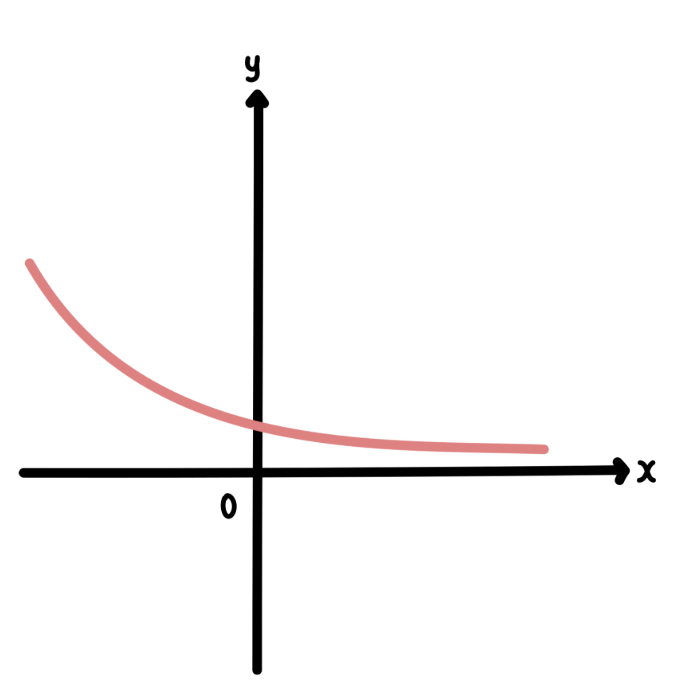
ちなみに、このような線形の場合は
- 0く b く 1
といった条件があります。
あるいは↓↓このような線形もあります。
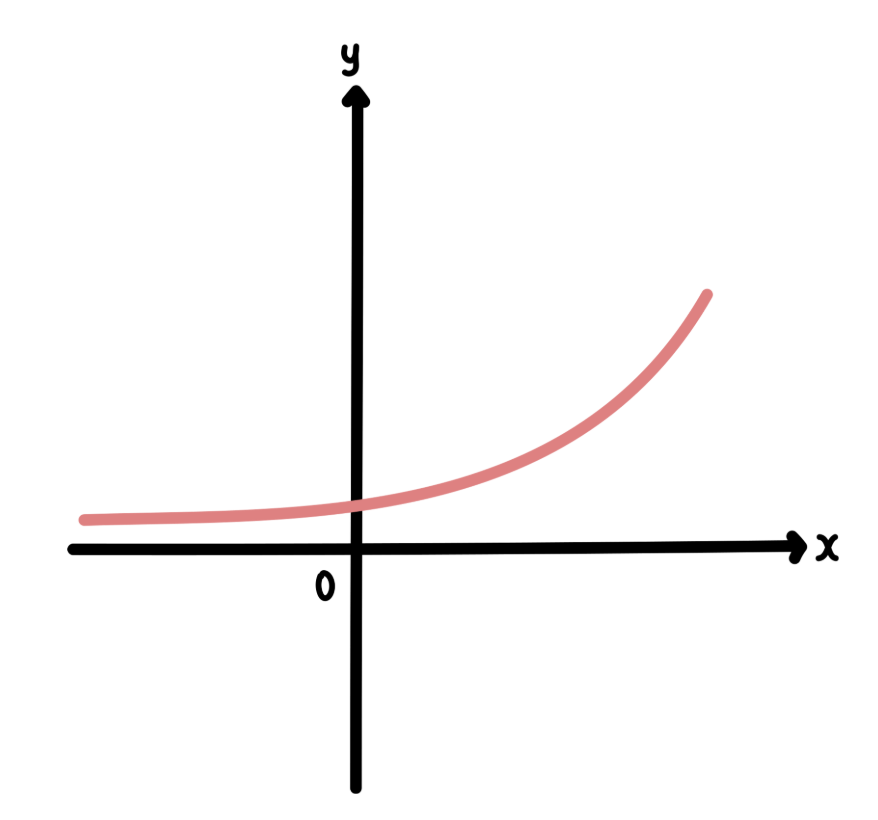
このような線形の場合は
- 1く b の
といった条件があります。
場合わけされている理由
さて、2つの線形を紹介しましたが、なぜ場合わけされているのかというと、このような回帰曲線を描く場合、回帰式は次の様になります。
- y=a×b
つまり、先ほどの条件は、この式の「b」の部分の条件によって、描く曲線が異なるために付与されているものだということです。
とはいえ、条件だけ示されても具体的なイメージが湧かないと思うので、実際に検証してみましょう(^^ゞ
具体例の検討
例えば
- y = 2 × 3
といった式を仮定してみます。
そして、この式の x に 1から5を代入してみると、yは以下の様になります。
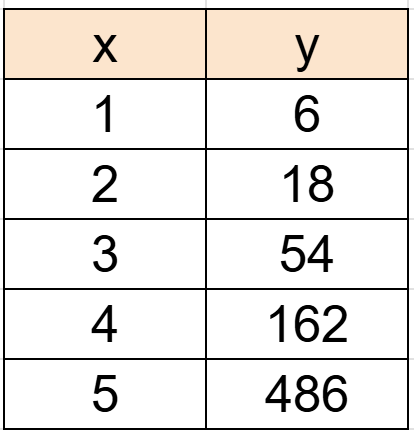
で 、 これをグラフ化すると・・・
↓↓こうなります
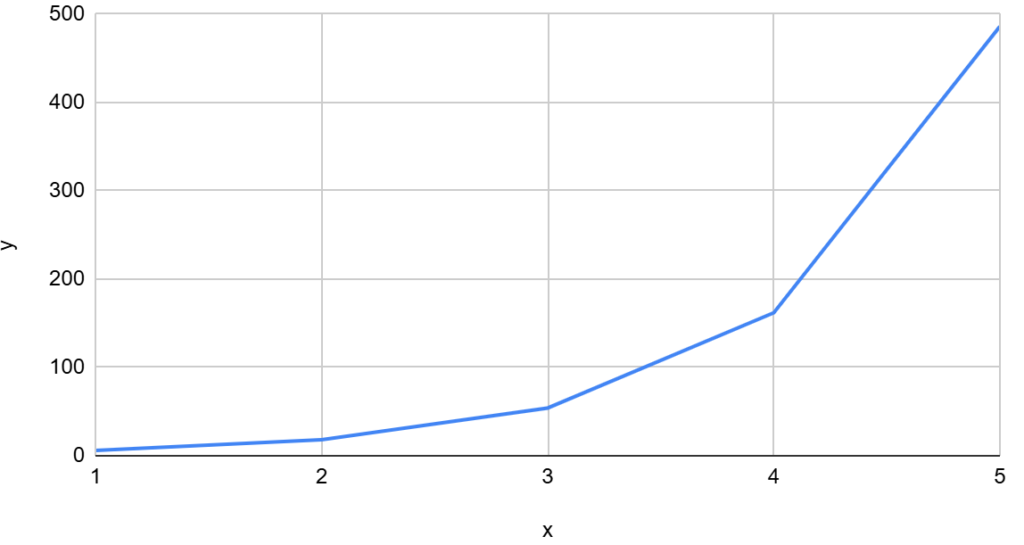
つまり 、 これは「 1く b 」 のときの式でした 。
0く b く 1 の場合
次に 「0く b く 1 」の場合を具体的に考えてみます。
これも
- y= 2 × 0.5
といった式を仮定してみます。
先ほど同様にこの式の x に 1から5を代入してみると、yは以下の様になります
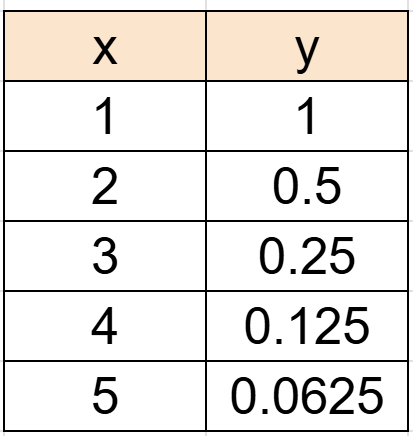
これをグラフ化すると↓↓ こうなります。
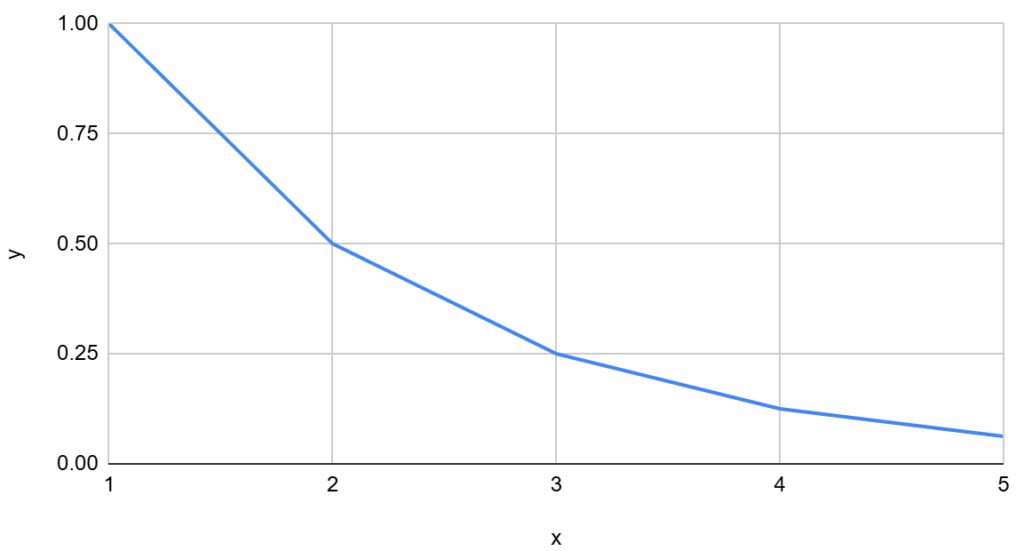
このように、指数曲線の様に非線形の回帰方程式が表す曲線を回帰曲線とよぶわけですね(^^)
まとめ
さて、いかがでしたでしょうか?
最後に、本記事の内容を振り返っておわかれです(^^)/
- 回帰曲線とは、指数関数的に描かれる回帰線のことを言う
- 回帰式は、「y=a×b」で示される。
- そのため、0く b く 1の場合、1く bで場合わけされている
ということなんですね~
それではまた♪



コメント