標準回帰係数とは？～わかりやすく～

この記事は、主に臨床心理士指定大学院生にむけた統計法学習シリーズです(^^♪

こんな疑問がある方は、ぜひご参考ください!(^^)!

結論～標準回帰係数とは？～

それでは、いつも通り結論からまいりましょう。

標準回帰係数とは、「回帰係数を標準化した値」です。

標準化の意味がわからない方は↓↓こちらをご参考ください。

これまでの学習で、回帰分析の求め方がわかりました。

そこで、回帰分析を行う目的を改めてふりかえると

この２つが大きく回帰分析を行う目的と考えられます。

そして、２つ目の目的である「説明変数の影響力」というのは

以下の式で言うと

回帰係数「a」のことを意味します。

そして、この「a」というのは、目的変数yに対する、説明変数xの影響力の大きさであることは過去記事で触れていますが、これをパス図で示すと以下の様になります。

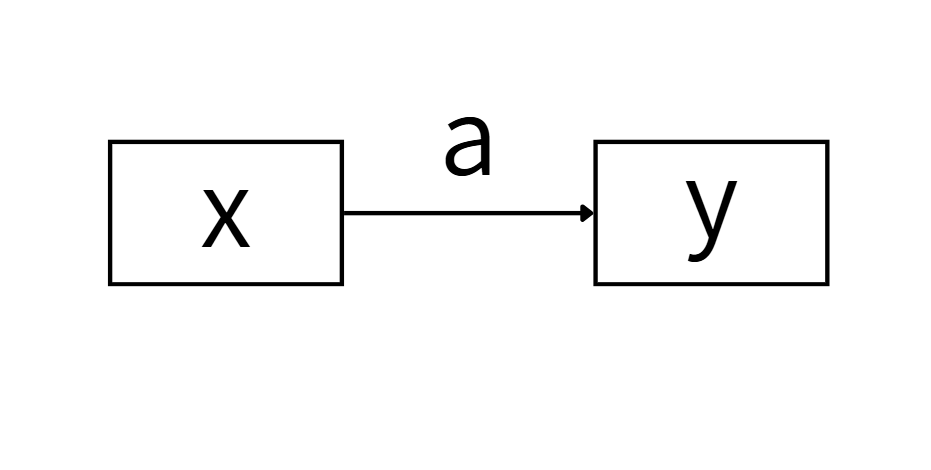
パス図の読み取りについても、過去記事で触れていますのでここでは割愛します。

ただし、ここでのポイントは、「a」が変数yに対する、変数xの影響を適切に表しているのかどうか？

という点にあります。

そして、その答えは

「決してそうではない」

ということです。

なぜなら、xとyでは単位が異なるからです。

例えば以下の様なデータがあるとします。

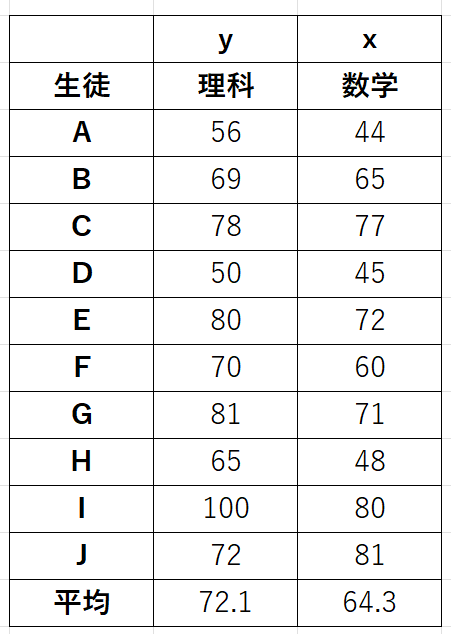
このデータでは、以下の様な設定をしています。

つまり、「数学の点数が高い生徒は、理科の点数も高いだろう」という推測のもと、回帰分析を実行しようと思います。

しかしながら、ここで、数学で65点とったBくんと理科で65点とったHくんに注目してください。

この65点という数値は一見同じですが、果たして、これらの数値が意味するところは同じなのでしょうか？

そもそもこれらの数値は高いのか？

それとも、低いのか？

その答えは「平均による」ということです。

具体的には、数学の点数の平均が「64.3」なので、Bくんの65点は高いです。

一方、理科の平均は「72点」であるため、Hくんの「65点」は低いと言えます。

この様に、基準が異なる中での影響力の比較は非常にあいまいなものになります。

そのため、これらを標準化した上で、求められた回帰係数を、目的変量yに対する、説明変量xの影響力の大きさにしましょうというのです。

そして！

その様にして求められた回帰係数のことを「標準回帰係数」とよぶわけです!(^^)!

さて、いかがでしたでしょうか？

最後に本記事の内容をふりかえってお別れです(^^)/