この記事は、心理系大学院生を対象とした統計法の学習ページです。
- 重相関係数ってなに?
- 重相関係数と重決定係数の違いがよくわからない
こんな悩みや疑問がある方はご参考ください( ˘ω˘)
動画で心理統計を学びませんか?
クリタマ勉強部屋では、修士論文に苦しんでいる心理系大学院生向けに、統計法の学習動画を提供しています(^^♪
今ならM-GTA記事も特典でついてきます
統計法の理解は長いことかかりますので、M1・M2の皆様は、ライフワークバランスを保つ選択肢の1つとしてぜひご活用ください。
結論~重相関係数とは?~
重相関係数とは、重回帰式の予測の精度を表す指標のことです。
「さて、以上の分散説明率とは別に、予測値と従属変数との相関係数も、予測の精度の高さを表す。この相関係数は、(説明変数と従属変数の)重相関係数と呼ばれる」
(引用:多変量データ解析法、P42. 8-9行目)
そして、重相関係数は具体的にどの数値のことを言っているかというと、以下の赤枠の部分です。

これは、Excelで重回帰分析を行った際の結果から切り取ったものです。
この画像だけもってこられても、イメージが湧かない人は↓↓をご参考ください。
重決定係数との違いは?
ただ、ここで気づいた人もいると思います。
「決定係数と何が違うの?」
ということです。
重回帰分析の読みとりのところでは「予測精度の高さ」をみる指標として「決定係数(分散説明率)」を扱いましたが、この疑問に関しては「どちらも同じ情報を扱っている」ということです。
「分散説明率=重相関係数の2乗(4.15)も常に成り立つ性質である。つまり、一見異なる重相関係数と分散説明率は同じ情報を担う.」
(引用:多変量データ解析法、P42. 2段落、6-7行)
実際にやってみましょう
じゃあ、なんで、情報を多くするのか?
それはよくわかりませんが、とりあえずその疑問はわきにおいておいて、本当に一致するのかどうか確認してみることにします。
先程の結果でいうと
- 重相関係数 = 0.982
- 決定係数 = 0.964
だったので、0.982 × 0.982 = 0.964 が成立すればよいということになります。
実際にやってみると、0.964324 になります。
たしかに、一致しました。
重相関係数=予測値と従属変数との相関係数
これも一応確認しておきましょう。
手順としては以下のとおりです。
- データから重回帰式を求める
- 重回帰式から予測値を求める。
- 実測値と予測値の相関分析を行う
これが先程の値と合致すれば、よいということですね。
では、実際にやってみましょう。
① データから重回帰式を求める
今回使ったデータが↓↓これ
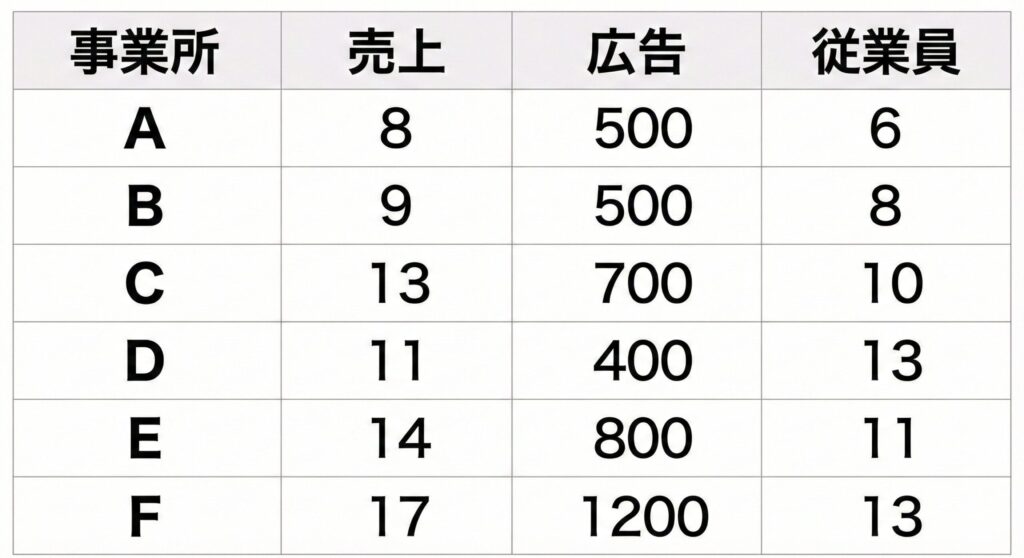
※カウンセリングルームA~Fの売上データ。売上=従属変数、広告と従業員数=独立変数
そしてこのデータで重回帰分析を行った結果が↓↓これ
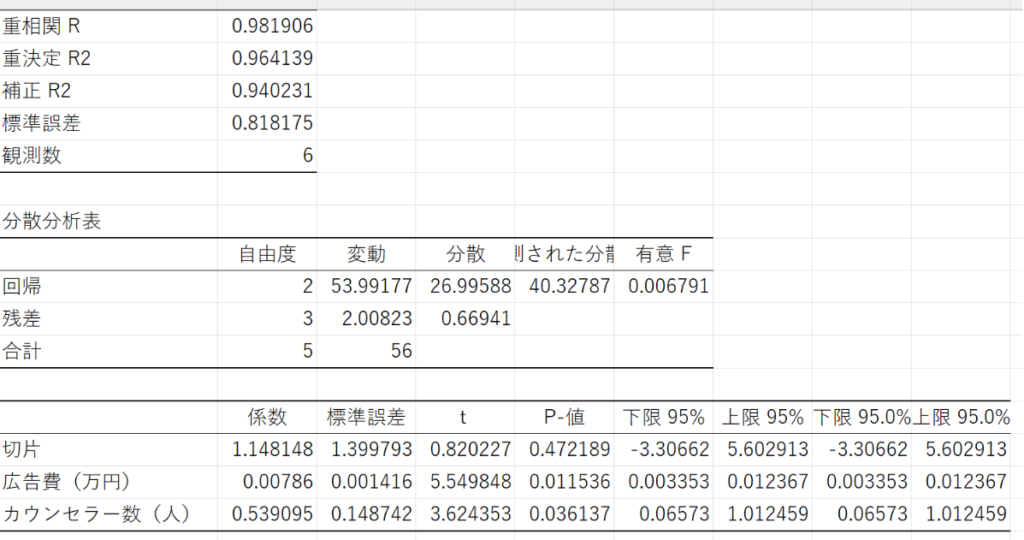
この結果から求められる式が↓↓これ
y = 0.00786x₁ + 0.53909x₂ + 1.148148
② 重回帰式から予測値を求める
重回帰式が求められたため、予測値を求めることが可能となりました。
そこで、先ほどの事業所A~Fでこの重回帰式を求めてみました。
それが↓これ

③ 実測値と予測値の相関分析を行う
さて、これで事業所A~Fの売上における、実測値と予測値がわかりました。
これで、相関係数を求めれば、それが「重相関係数」ということになります。
やってみましょう。
で実際に得られた相関表が↓これ
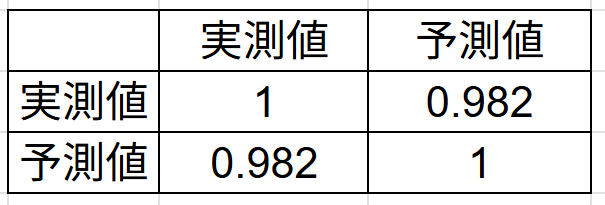
最初にみた↓この出力結果、しっかり一致していることがわかります。

※相関分析を行うプロセスを知りたい方は、動画コンテンツを申請してください。
まとめ
さて、いかがでしたでしょうか?
重相関係数について少しは理解が深まったでしょうか?
最後に本記事の内容を振り返っておわかれです(^^)/
- 重相関係数とは、重回帰式の予測の精度を表す指標のこと
- 重相関係数と重決定係数は同じ情報を担っている(重相関係数² = 決定係数)
- 重相関係数は、予測値と従属変数(実測値)との相関係数と一致する
ということなんですね~
それではまた(^^ゞ
こちらの内容を動画で学びたい方は
※ページの最下部からこの記事の感想をコメントしてください。その後、パスワードをお送りします(^^ゞ
参考
こちらの記事を作成にする上での参考文献です(^ω^)
①多変量解析がわかる
②多変量データ解析法
③例題とExcel演習で学ぶ多変量解析








コメント