この記事は、心理系大学院生を対象とした統計法の学習ページです。
- 重回帰分析における偏回帰係数ってどう解釈するの?
- 単回帰分析と重回帰分析の違いがよくわからない
- 回帰係数の読み取り方について勉強したけど腑に落ちない
こんな悩みや疑問がある方はご参考ください( ˘ω˘)
動画で心理統計を学びませんか?
クリタマ勉強部屋では、修士論文に苦しんでいる心理系大学院生向けに、統計法の学習動画を提供しています(^^♪
今ならM-GTA記事も特典でついてきます
統計法の理解は長いことかかりますので、M1・M2の皆様は、ライフワークバランスを保つ選択肢の1つとしてぜひご活用ください。
重回帰分析における偏回帰係数の解釈
重回帰分析における偏回帰係数の読みとりに関しては、重回帰分析の読み取りで扱った通りです。
ただ、ここでは、回帰分析と重回帰分析の解釈の違いを明らかにします。
単回帰分析の場合
例えば、あるダイエットのデータから、運動量と体重の増減において単回帰分析を行ったところ、以下のような結果が得られたとします。
- 体重 = 0.5 × 運動量
これはつまり、「運動量が増えると、体重が増える」ことを意味しています。
しかし、これだけみると違和感があります。
なぜ、こんなことになったのでしょうか?
おそらく、この単回帰分析のデータを提供してくれた人たちは、「それ以上に食べている」からだと考えられます。
運動量が増えた → その結果、食事量が増えた → それで、最終的に体重も増えた
という様な流れになったのではないか?ということですね。
つまり、ここでのメッセージとして
単回帰分析は、「その結果、食事量が増えた」を考慮していないということです。
重回帰分析とは異なり、相関係数や単回帰分析の回帰係数は「素材」と「売れ行き」のように2つの変数だけに基づくので、これらに他の変数が影響を及ぼす影響を除いた結果までは、示せない。
(引用:多変量解析、P46. 2段落、1-2行目)
単回帰分析は、「木を見て森を見ず」 ということですね。
重回帰分析の場合
一方、先ほどのデータに基づいて、重回帰分析を行うと
- 体重 = -0.2 × 運動量 + 0.35 × 食事量
この様な式になります。
ここで求められた式を見る限りは「運動量が増えれば、体重が減る」 ということが読み取れます。
これはなぜなら「食事量の影響も考慮している」からです。
この様に、重回帰分析の偏回帰係数数を解釈するときは、「複数の変数の影響を考慮している」 ということを念頭においてよみとることが重要なわけです。
そして、仮に、単回帰分析で考えられた
運動量が増えた → その結果、食事量が増えた → それで、最終的に体重も増えた
という仮説が正しいとすれば各変数の相関は次のようになることが想定されます。
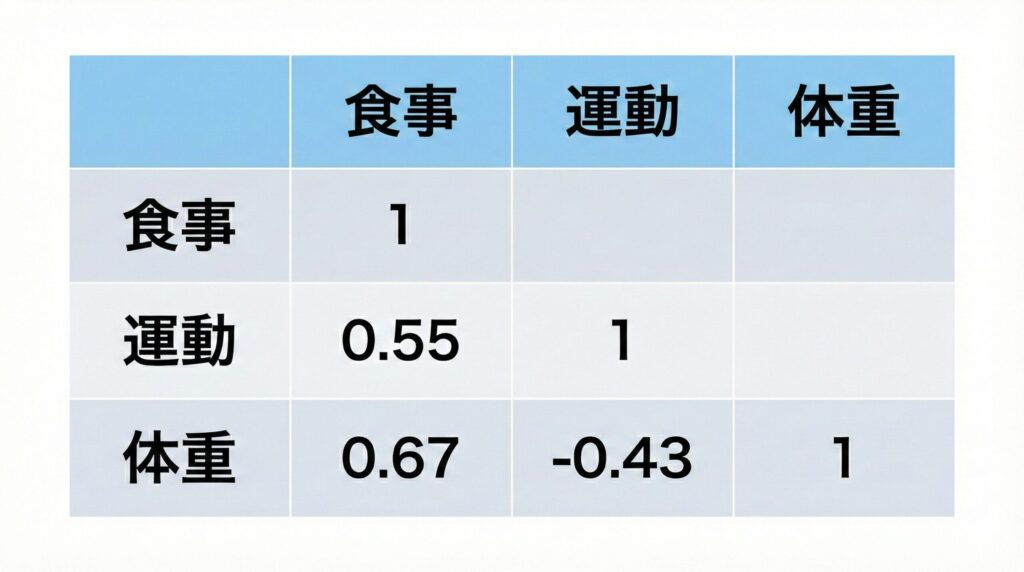
この表から言えることを整理すると
- 食事と運動で正の相関 → 運動が増えると食事も増える
- 食事と体重で正の相関 → 食事が増えると体重が増える
- 運動と体重で負の相関 → 運動が増えると体重が減る
つまり、2と3はどちらも納得がいくものですが、1も考慮すると、結果「(食事 > 運動)= 体重増」で「運動量が増えると、食事も増えて結果的に食事量が運動量を上回り、体重が増える」ということになってしまったのだと考えられるわけです。
まとめ
いかがでしたでしょうか?
重回帰分析における偏回帰係数の解釈について少しは理解が深まったでしょうか?
最後に本記事の内容を振り返っておわかれです(^^)/
- 単回帰分析は、2つの変数だけに基づくので、他の変数の影響を考慮できない(「木を見て森を見ず」)
- 重回帰分析では、複数の変数の影響を考慮した解釈ができる
- ダイエットの例では、単回帰分析では「運動量が増えると体重が増える」という結果になったが、重回帰分析で食事量を考慮すると「運動量が増えると体重が減る」という正しい解釈ができる
ということなんですね~
それではまた(^^ゞ
参考
こちらの記事を作成にする上での参考文献です(^ω^)
①多変量解析がわかる
②多変量データ解析法
③例題とExcel演習で学ぶ多変量解析







コメント