この記事は・・・
前回までの振り返り
この記事は、こちらの記事の続きとして作成ています。
そして、要点をまとめると
- 回帰曲線は「y= a x b 」の式であらわされる。
- グラフの形状は、指数関数的に数量が変化する
以上が、回帰曲線の特徴として挙げられていました。
では、このような特徴をもつ回帰曲線は、どのように分析をするのでしょうか?
結論~回帰曲線の対応~
結論としては次の通りです。
- 「線形」回帰分析ができる様にデータを整える
- その上で、通常の回帰分析を行う
この2点を踏まえて、実例をみていくことにします!(^^)!
具体的には、どんなデータを用いるのか?
例えば 、以下の様なグラフがあるとします。
- 横軸 ・ ・ ・ 年号
- 縦軸 ・ ・ ・ 売上
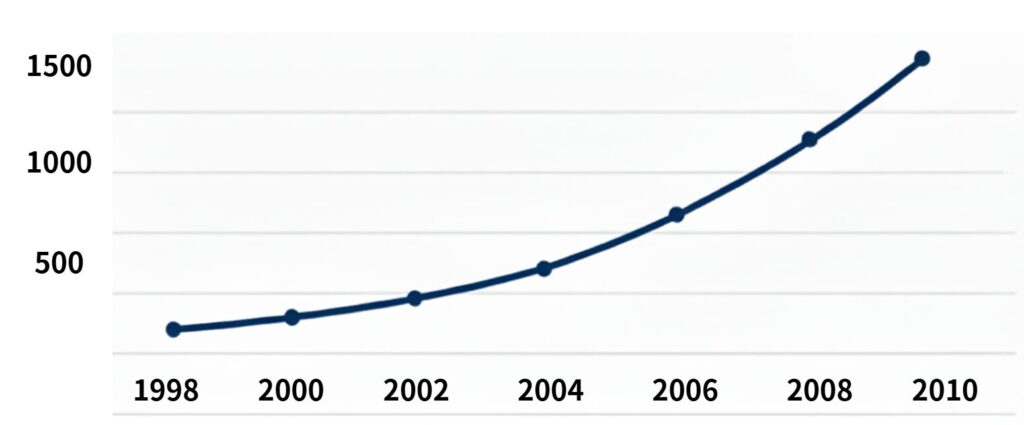
普通
普通は 、回帰分析を実施する散布図は↓こんなイメージですよね。
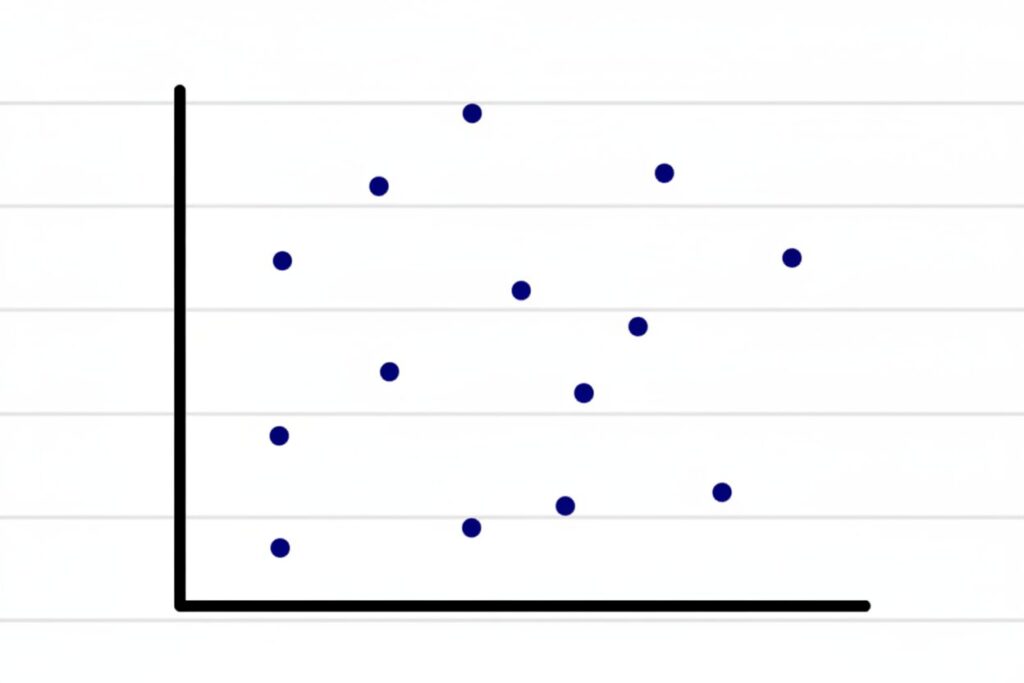
見比べてみると違いがよくわかります(^^)
いわゆる成長曲線です
では、話を戻しましょう。
先程の様なグラフを描く場合、非線形の回帰分析を適用することになります
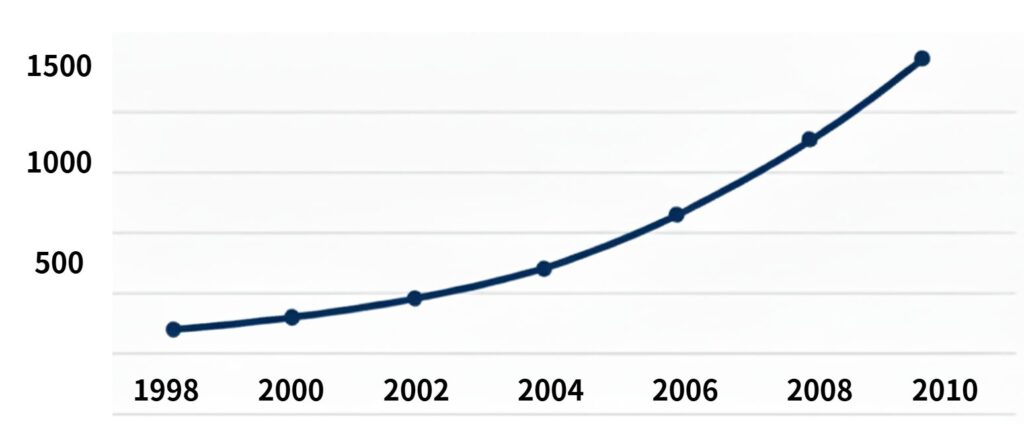
つまり 、 いわゆる「成長曲線」がその対象になるということです。
例えば、
- 植物や動物の成長をあらわすグラフ
- 自動車の販売台数をあらわすグラフ
などの様に、急に、物が売れたり普及したりする現象を説明するのに用いられるようです。
実際に回帰分析を行ってみる
冒頭で述べた通り、非線形モデルは扱いが難しいので、変数を変換して、まず線形化するところからはじめます 。
先程のグラフ は 、 以下のデータから作成したものです。
| 年 | 販売台数 |
| 2000年 | 207 |
| 2001年 | 238 |
| 2002年 | 325 |
| 2003年 | 439 |
| 2004年 | 505 |
| 2005年 | 577 |
| 2006年 | 722 |
| 2007年 | 879 |
| 2008年 | 938 |
| 2009年 | 1364 |
対数線形モデルの場合、 回帰式は・・・
- y = a × b
のような方程式になります。
そして「1 く b」のときに、このような曲線を描くという話でした。
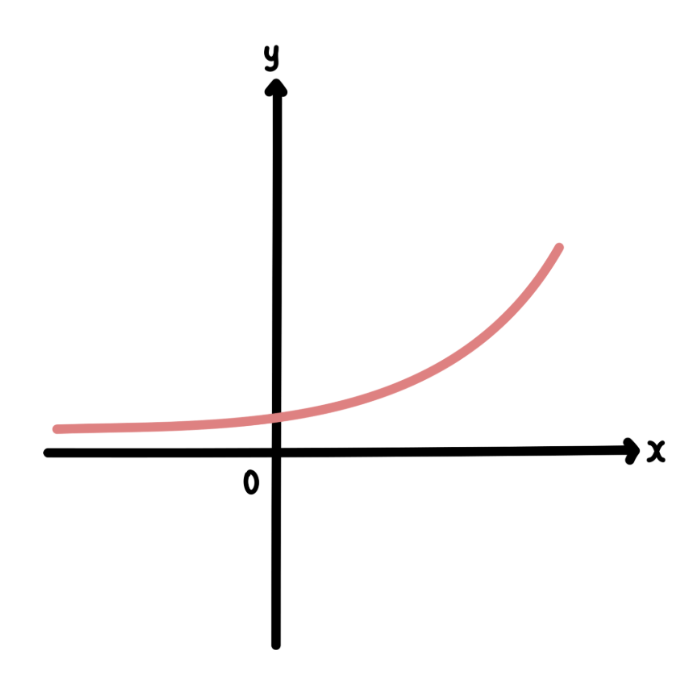
つまり、先程のデータも
「y = a x b」式で表わすことができるということです。
そして、この式を「線形」に するということは、通常の回帰分析で用いられる
「y= a x + b」の式に変換しようということです。
ただし、それを地力でやろうとすると、数学的な話をしないといけません。
そこで 、 今回はExcelを使ってやってみることにします。
GROWTH関数を使う
ここでは、GORWTH関数を用いて、予測結果を返す手続きを紹介します。
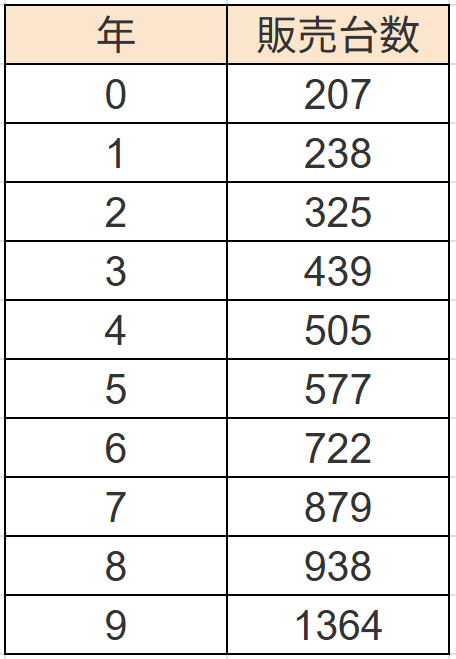
こちらはExcel(スプレッドシート)ように、データを入力した表です。
年号がデータの取り扱い下一桁のみになっています。
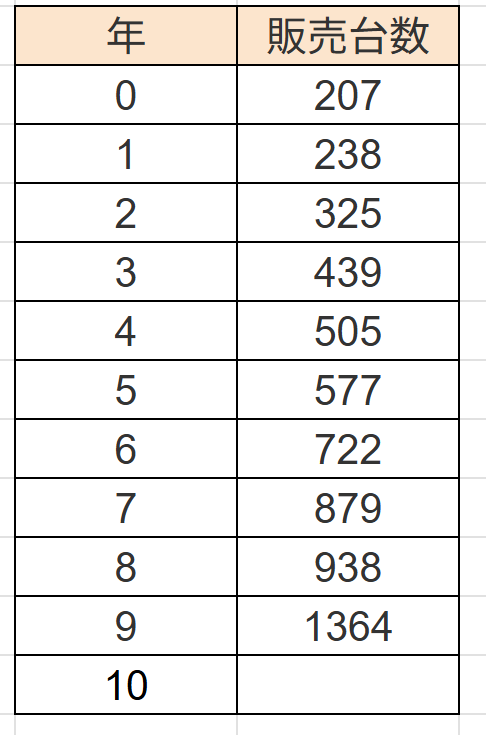
ここに、出力したい、2010年の行を作成します。
ここに=GORWTHを入力。
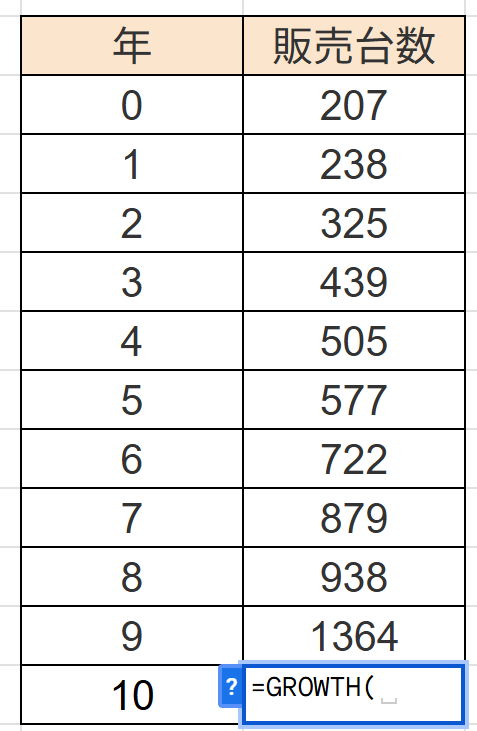
関数の( )内は、以下のように範囲を指定します。
=GROWTH(既知のy, 既知のx, 新しいx)
つまり、↓↓こういうこと
- 既知のy・・・販売台数
- 既知のx・・・年代
- 新しいx・・・2010年のセル
実際にやってみましょう。
まず、既知のxは↓↓このように、「C3:C12」を範囲として指定し、「,」で区切りましょう。
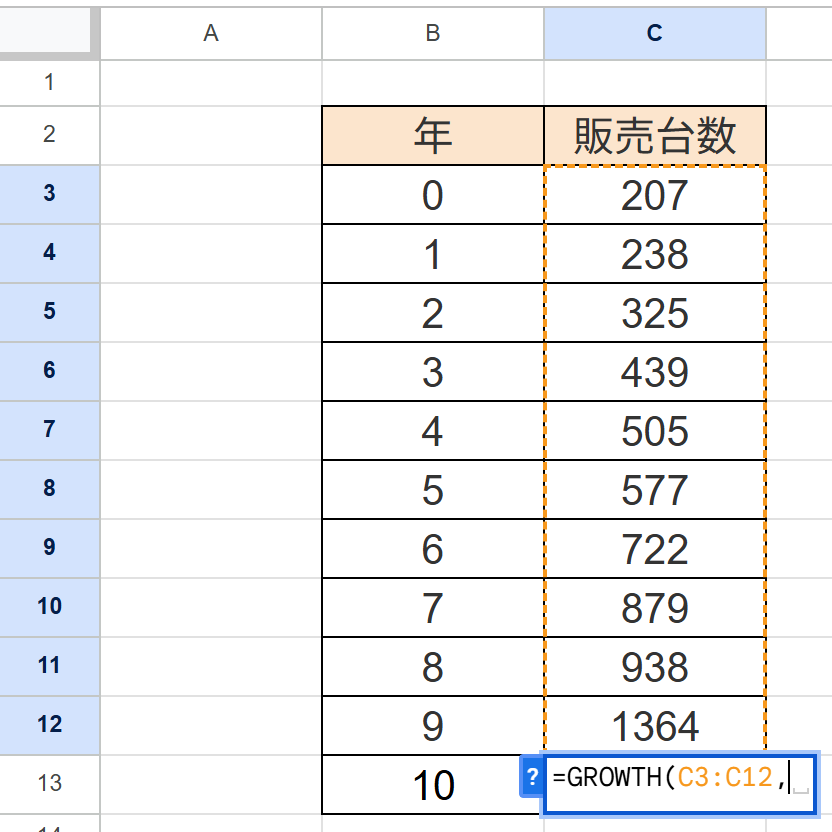
次に、既知のxは↓↓このように「B3:B12」を範囲として指定し、同様に「,」で区切る。
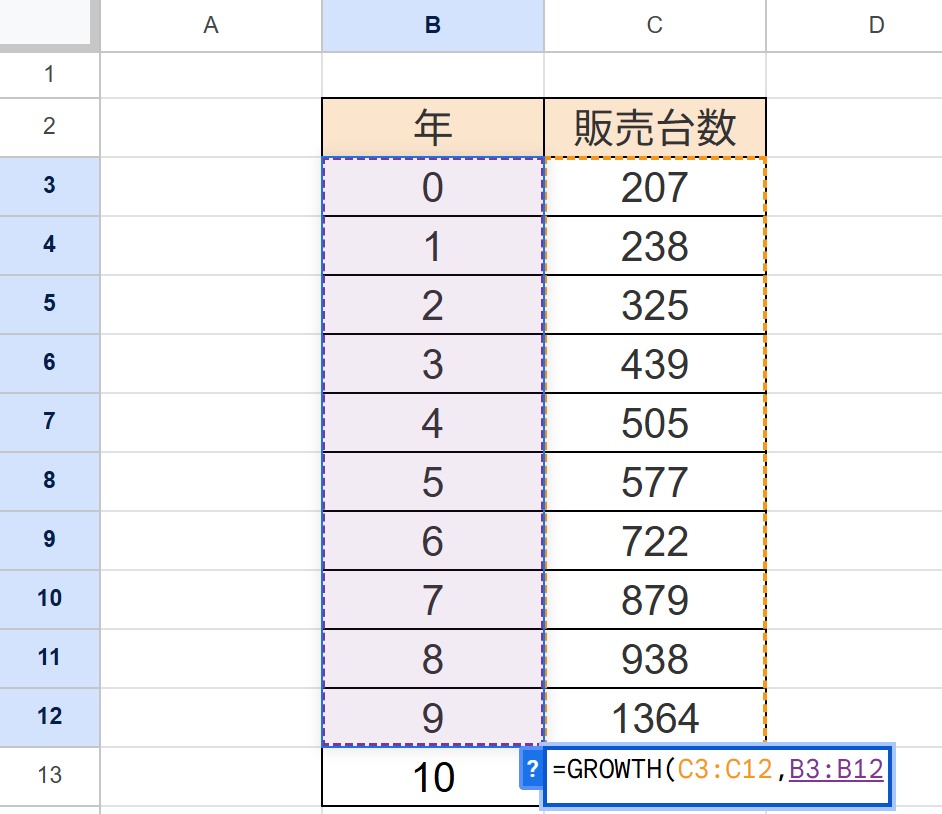
最後に、新しいyとして、「B13」を指定してエンター。
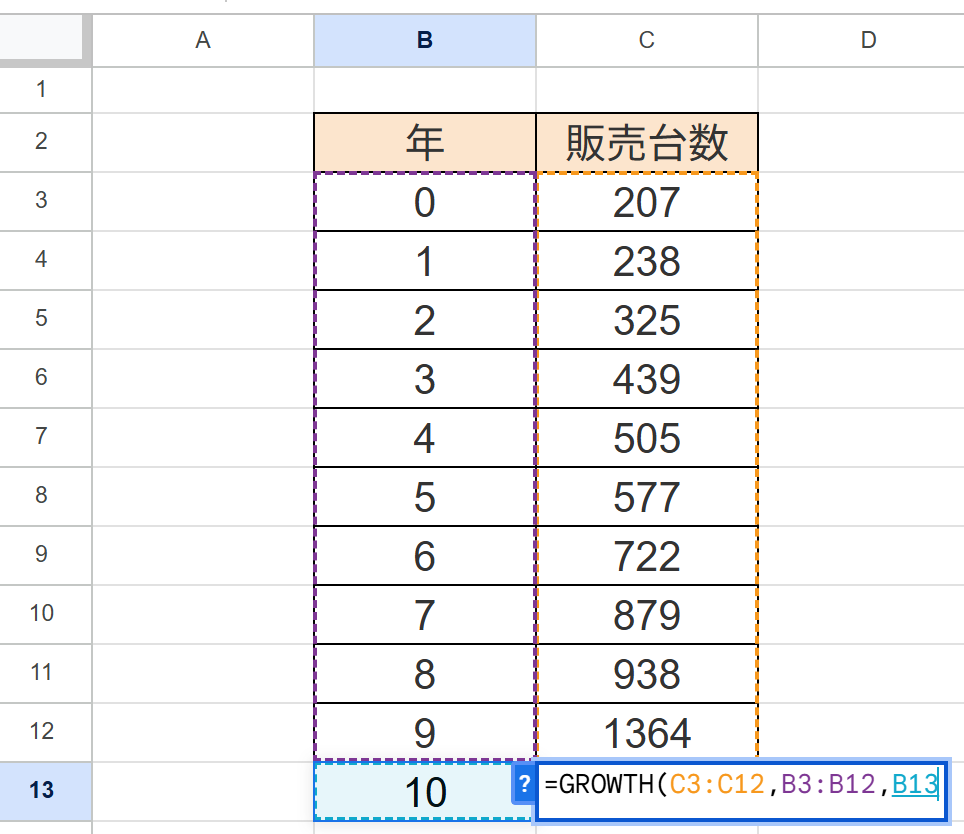
すると・・・
↓↓このように値が返ってきますので、これで完了です(^^)/
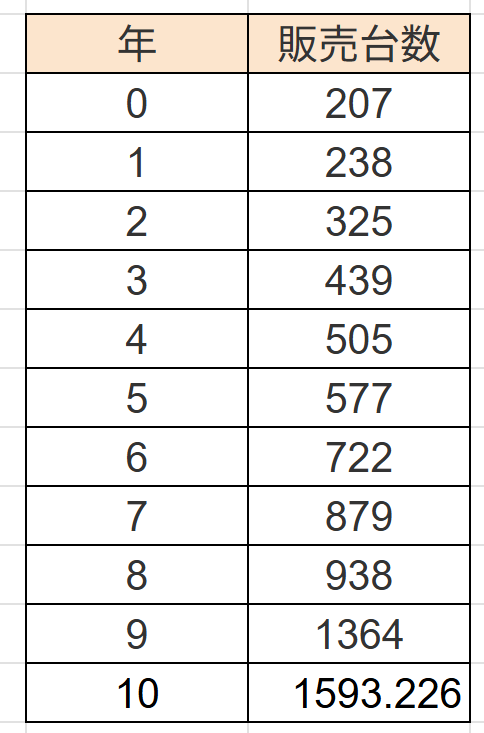
予測範囲を広げると、↓↓こうなります
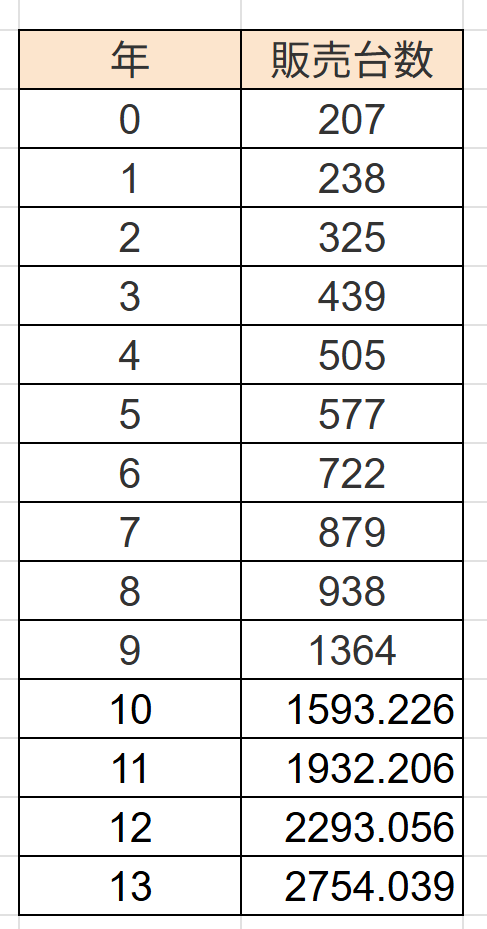
以上回帰曲線の場合の対応方法となります。
まとめ
いかがでしたでしょうか?
回帰曲線の場合の対応方法いついて理解は深まったでしょうか?
最後に、本記事の内容を振り返ってお別れです(^^)/
- 回帰曲線の分析を行う場合、まずは「線形」回帰分析ができる様にデータを整える
- その上で、通常の回帰分析を行う
- 普通にやると数学的な知識が必要になるため、GROWTH関数を使うと簡単
ということなんですね~
それではまた(^^ゞ



コメント