この記事では、回帰分析を求める際の方法論である、「最小二乗法」についてまとめておきます。
- 最小二乗法ってなに?
- なんで2乗するの?
こんな疑問がある方は、ぜひご覧ください(^^ゞ
結論~最小二乗法とは~
結論を最初に申し上げますと、最小二乗法は、データ個々と回帰直線のズレが最も小さくなるような値を求める方法のことを言います。
これだけきいて分かる人はいないと思うので、とりあえずそのことを念頭に読み進めてみてください。
前回までのおさらい
最小二乗法を説明するにあたって、回帰直線のおさえておきたい特徴は2つあります。
- 回帰直線はxとyの変数の平均を通る線
- 回帰直線は、個々のデータと回帰直線のy軸のズレを合計した値が最小になる線
ということですね。
で、この2が、つまり最小二乗法のことです。
以上を踏まえて、最小二乗法について解像度を上げていきます。
ちなみに、「データのズレ」の意味にいては、過去記事をご参考ください。
なぜ、二乗するのか?
そして、前回までの内容で、「最小」の意味はわかりました。
データと回帰直線との距離を最小にするということです。
しかし、それだけでは「二乗」の意味がよくわかりません。
一体何を二乗するのか?
なぜ二乗するのか?
ということです。
まず、「何を二乗するのか?」という点に対する答えですが、その答えは
↓↓こちらの部分を二乗することを意味します。
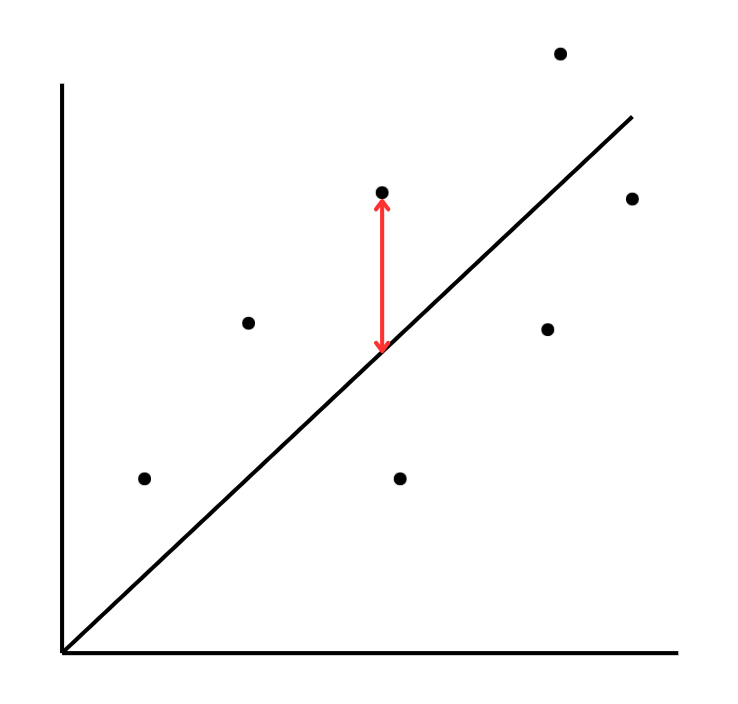
つまり、「個々のデータと、回帰直線とのy軸のズレを二乗してたし合わせた上で、その値が最小になる線=回帰直線」ということです。
試しに、先ほどの1つのデータだけ二乗してみることにします。
すると、イメージ的には↓↓こうなります。
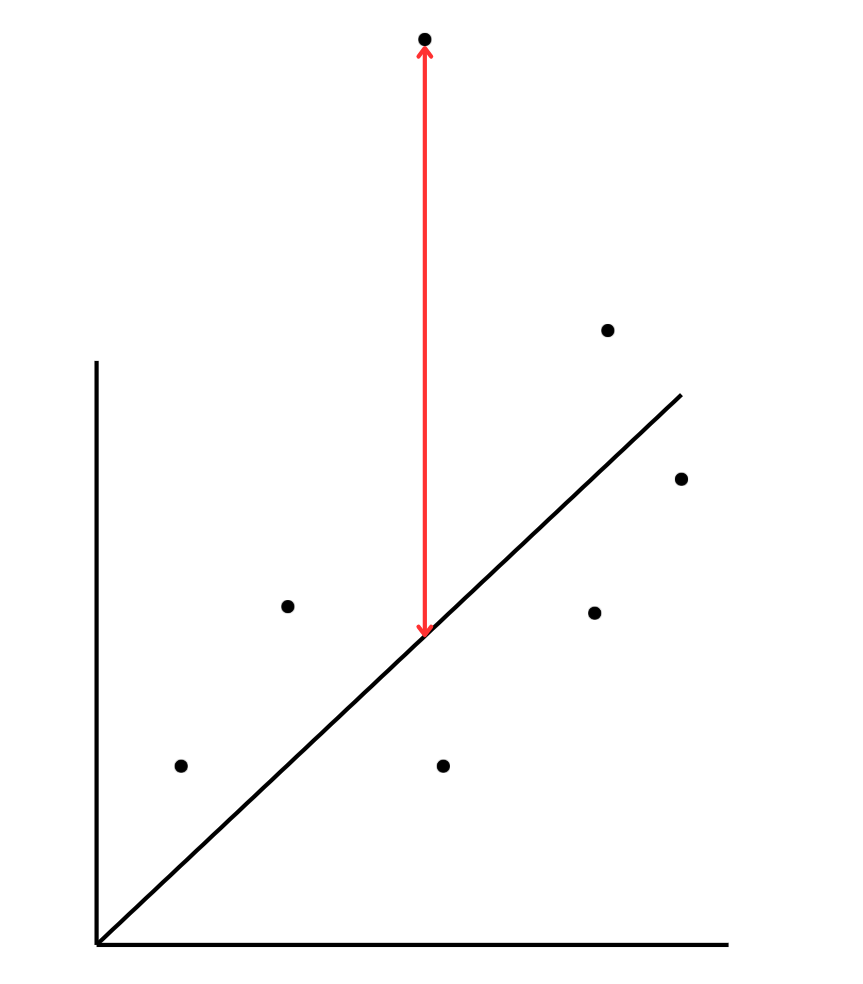
当然ながら、直線との差が大きくなりますね。
なぜ、二乗するのか?
なぜこんな面倒なことをするのか?
それは、「マイナス」をなくすためです。
例えば、以下のデータと回帰直線の差を求めると値がマイナスになります。
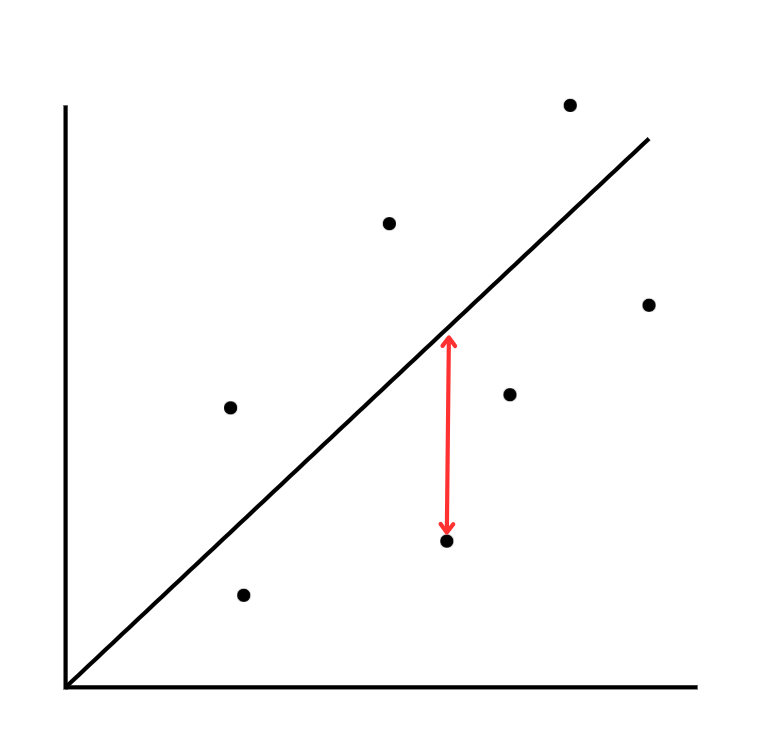
なぜなら、この差を求める式は
- (個々のデータyの値)−(回帰直線のyの値)
だからです。
y軸の差を求めるのだから、回帰直線より上の位置にデータがあれば、「正」だし、低い位置なら「負」になります。
ですので、仮に二乗しないまま合計すると「0」になるだけです。
だから、二乗するのです。
というわけで、さきほどのグラフのデータを全て二乗すると
↓↓こんなイメージです
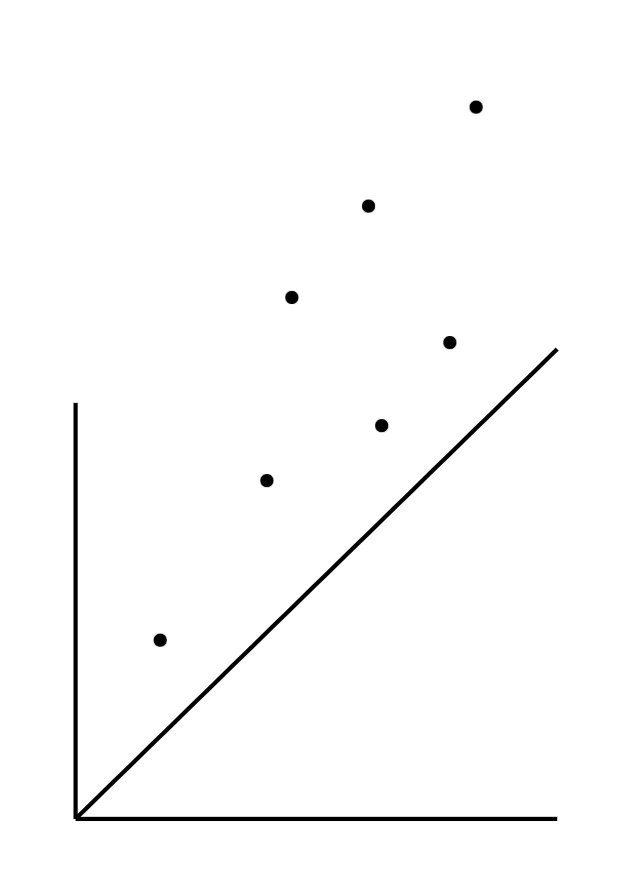
全てのデータが回帰直線よりも上に位置した状態になりましたね。
これで、全ての値を「正」として扱えるわけです。
言い換えれば、合計しても「0」にはなりません。
だから、「個々のデータと、回帰直線とy軸とのズレを二乗して、たし合わせたうえで、その値が最小になる線=回帰直線になる」というわけです。
この様にして求められる回帰直線y=ax+bなる式が求められると、傾きaと切片bがわかることになります。
では、最小値はどういう理屈で求めるのか?
最小値を求めるのはわかったと。
しかし、その理屈がよくわからないという方向けにもう少し深堀してみたいと思います。
以下は先ほどの散布図を二乗する前のものですが、ここで、矢印に示した仮の座標を仮に(x1,y1)とします。
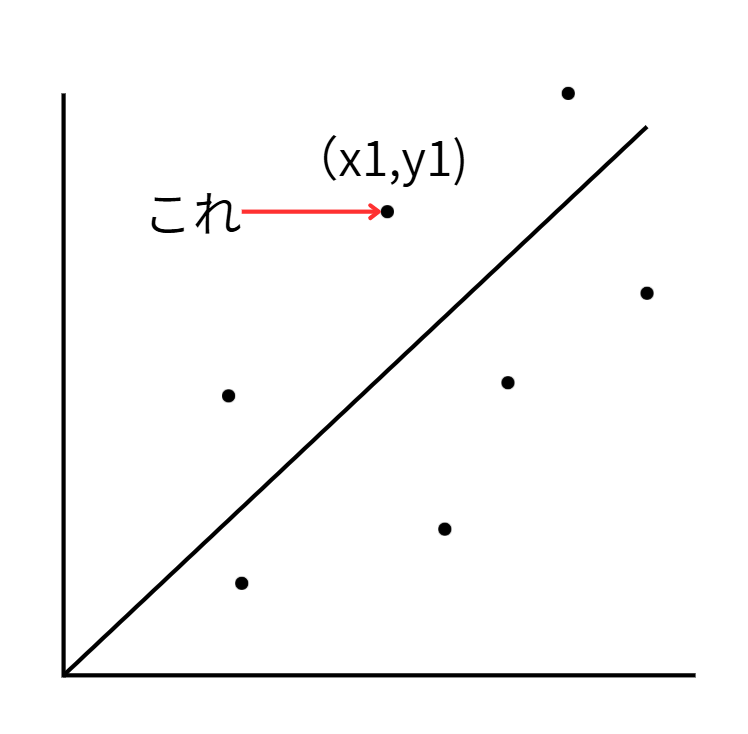
すると、↓↓こちらの回帰直線上にある点のx軸の座標は同じx1ということです。
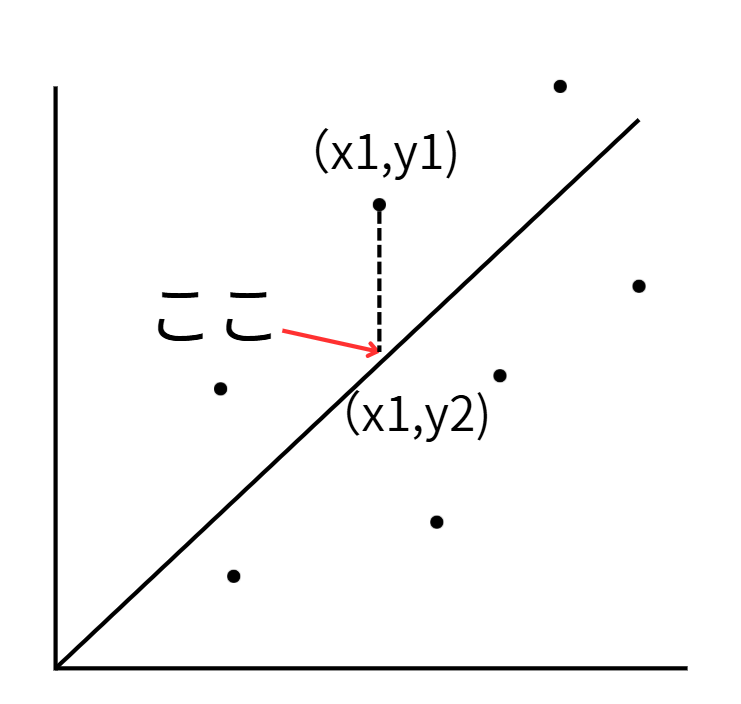
ただし、y軸の座標は異なるので、ここでは(x1,y2)とします。
ここで、回帰直線を求めるために、実際のデータとy軸の差を求めると「y1-y2」といった引き算をする必要があります。
そして、回帰直線の式は以下のようにあらわされるといった前提がありました。
- y= ax+b
そして、この式は、言い換えれば以下のようになります。
※x_・・・xの平均値、y_・・・yの平均値です
- y=a(x-x_)+y_
これが理解できない方は、回帰直線の特徴①に詳しく書いてます。
そして、ここに、(x1, y2)を代入してみると次のようになります。
- y2= a(x1-x_)+y_
さらに、これを展開すると次の通りです。
- y1-y2 =y1 – {a(x1-x_)+y_}
そしてさらに、右辺を整理すると次の通りです。
- y1-y2 =-a(x1-x_)+y1-y_
もはやついてこれなくなった人もいるかもしれないのですが、現在位置を確認しておくと一体今、何の話をしているのとかいうと・・・
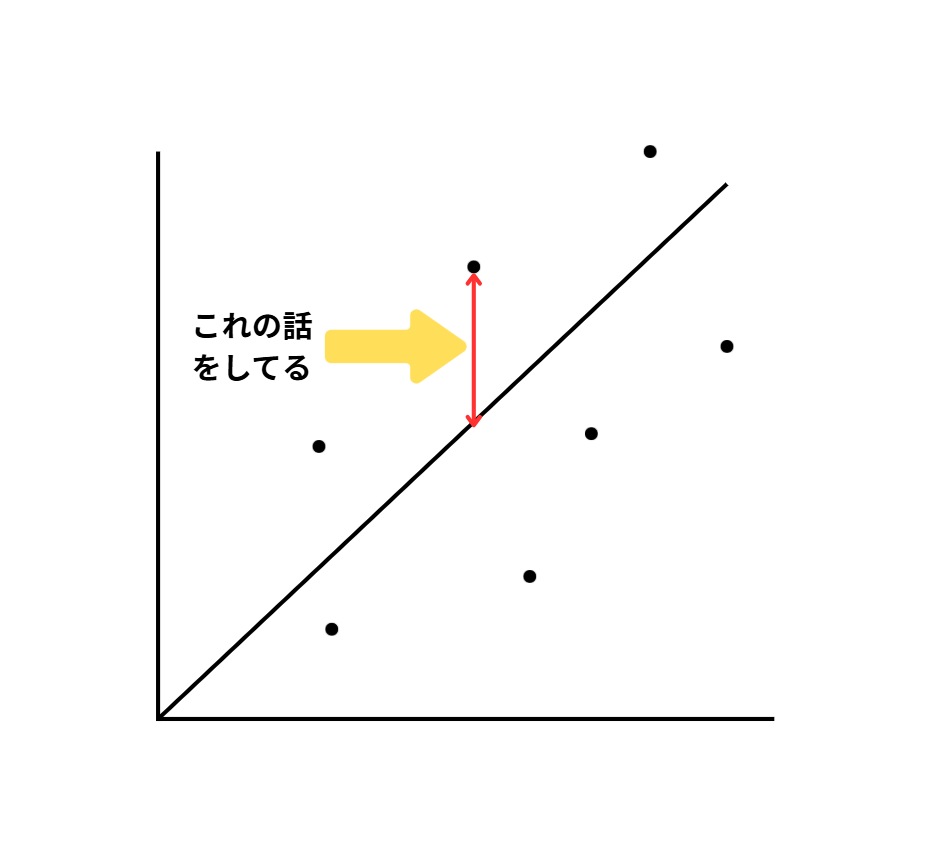
つまり、「データと回帰直線の距離」についてです。
なにゆえ、こんなわけのわからん計算をしてるのか?
これが回帰直線を出すための最小二乗法のプロセスだからです。
というのも、「y1-y2」は上図に示したとおり
「あるデータと回帰直線のズレ」です。
そして「そのズレを二乗した値の総和の最小値をだす=最小二乗法」でしたよね?
つまり、「じゃぁ、具体的にどうやって最小値を計算するの?」というのが、今ここでの話です。
で、話を戻しますが、「(y1-y2)が回帰直線とデータの距離」ということは、以下の計算をすると
- (y1-y2)× (y1-y2)
↓↓こうなるわけです。

この図を忘れてしまった方は、この記事を読み直しみてください。
そして、以下のような式をさきほど導きました。
- y1-y2 = -a(x1-x_)+y1-y_
ということは・・・
- (y1-y2 )二乗 = {-a(x1-x_)+y1-y_ }二乗
このような式がなりたつわけですね。
ポイントは左辺を二乗したら、右辺も二乗ってことです。
そして、ここで最も大事になってくるのが、この式を展開すると2次式になるということです。
なぜなら
二次式を見える可すると、↓↓こんな形になります。
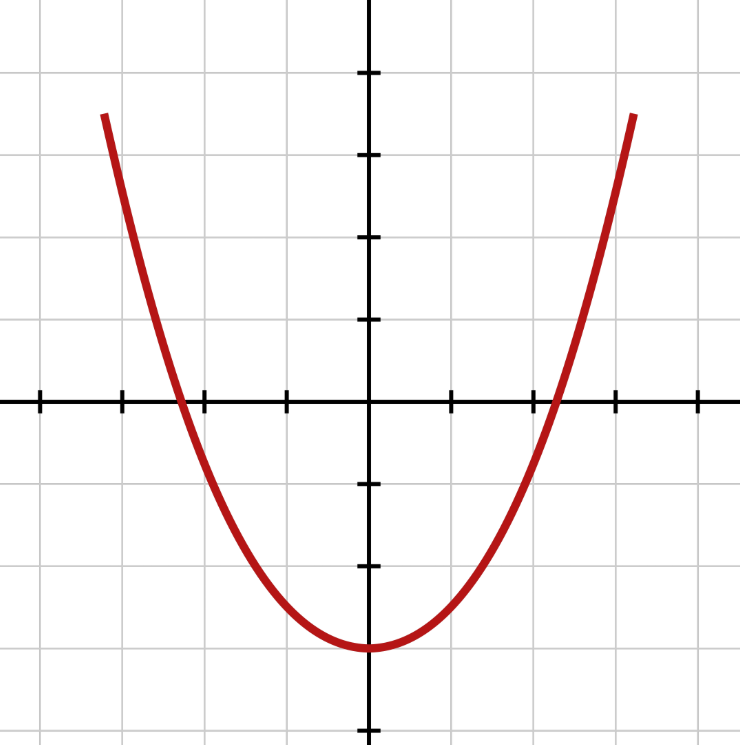
つまり、最小値は
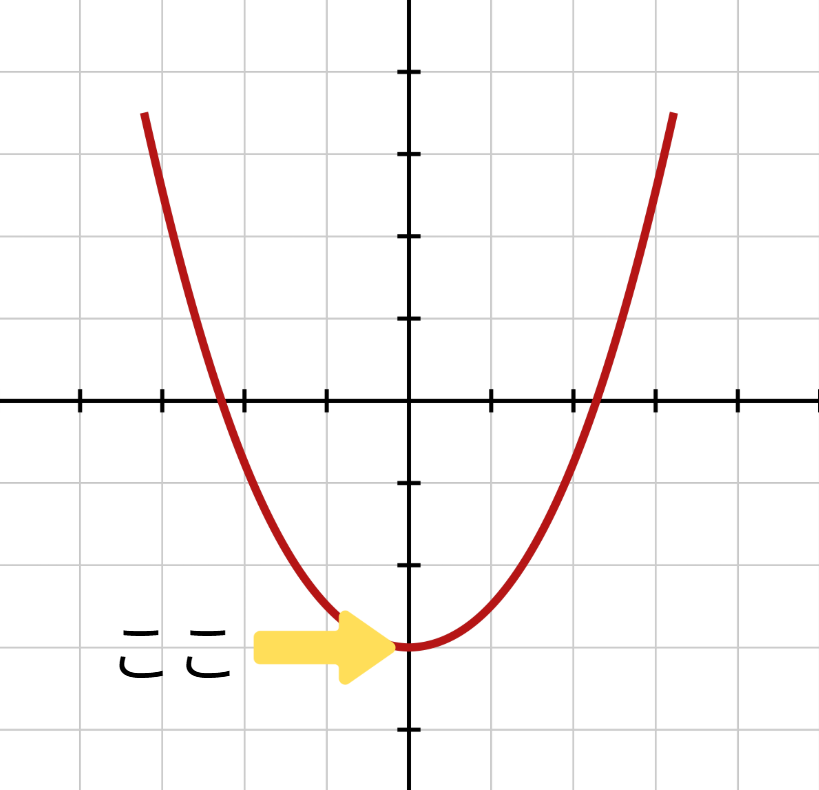
ですよね?
つまり、以下の「二乗した式」をとくことが「その最小値」を求めることに繋がるわけです。
- (y1-y2 )二乗 = {-a(x1-x_)+y1-y_ }二乗
↑この右辺を展開するために、以下の公式を使います。
- (A+B)二乗 = A2+2AB+B2
この公式のAとBをそれぞれ次のように起きます。
- A=-a(x1-x_)
- B=x1-y_
とすると以下のようになります。
- {-a(x1-x_)}2乗-2a(x1-x)(y1-y_)+(y1-y_)2乗
で、最終的には
- a2乗(x1-x)2乗-2a(x1-x)(y1-y)+(y1-y)2乗
となります。
で、何度もいいますが、この式はこの式は(y1-y2)の二乗なので・・・
つまり、↓↓こうなった状態です。

このずれの最小値は
- a2乗(x1-x)2乗-2a(x1-x)(y1-y)+(y1-y)2乗
この式を解くことで求めることができます。
そして、これは二次関数なので、最小値は

でした。
ただし、ここまでの説明は、あくまでもデータの1つをとりあげたにすぎないので、
↓↓このように
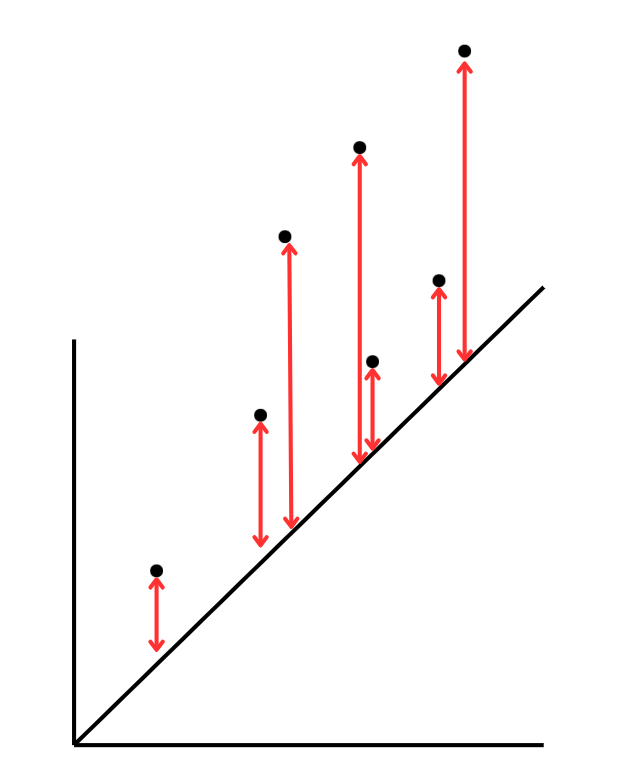
全てのデータと回帰直線のズレの最長値を求めて足し合わせた数値が
「全体の最長値」ということになります。
なぜなら、このデータの1つ1つのズレはさきほど説明したとおり、「2次関数」なわけです。
なので、それぞれの最長値を求めるということは、上記の二次関数の頂点を求めて足し合わせると言う話になります。
だから、「回帰直線とデータの個々のズレを二乗して足し合わせた数の最小値」が「最小二乗法」ということなんですね。
実際に最小二乗法の計算の様子が知りたい方は↓↓こちら
まとめ
それでは、最後に、本記事の内容を振り返っておわかれです(^^)/
- 最小二乗法とは、回帰直線とデータの個々のズレを二乗して足し合わせた数の最小値を求めることで、回帰直線を求める方法
- 最小二乗法では、データと回帰直線の差を二乗する
- なぜ、データと回帰直線の差を二乗するのかというと、「マイナス」の値をなくすため。
- 最小二乗法では、マイナスの値が残ったままデータを足し合わせると答えが「0」になってしまう。
- また、データを二乗するということは、式を二次関数に変換することでもある。
- 二次関数は、最小値が明確にきまっている。
ということなんでね~
それではまた(^^ゞ
参考
最後に、本記事を作成する上での参考文献を紹介します(^^♪
①多変量解析がわかる
②図解雑学 多変量解析







コメント