この記事は、心理系大学院生を対象とした統計法の学習ページです。
- 多重共線性ってなに?
- 重回帰分析の結果がなんだかおかしい…
- 相関をチェックしたはずなのに、なぜか分析がうまくいかない
こんな悩みや疑問がある方はご参考ください( ˘ω˘)
動画で心理統計を学びませんか?
クリタマ勉強部屋では、修士論文に苦しんでいる心理系大学院生向けに、統計法の学習動画を提供しています(^^♪
今ならM-GTA記事も特典でついてきます
統計法の理解は長いことかかりますので、M1・M2の皆様は、ライフワークバランスを保つ選択肢の1つとしてぜひご活用ください。
多重共線性(マルチコ)とは?
重回帰分析を行う際、大きな弱点のひとつとなるのが多重共線性です 。
多重共線性とは、説明変数(独立変数)同士の間に強い相関があるとき、回帰係数の符号が予想に反したりするような現象のことを指します 。
重回帰分析の弱点の1つは、「説明変数間の相関が強すぎる場合に、分析結果が過度に不安定になる」ことであり、「説明変数間の相関が強すぎる」という性質を、多重共線性と呼ぶ
(引用:多変量データ解析法 P52. 1-3行)
多重共線性の具体例をイメージ
例えば、ある店舗の売上に対する影響を調べるために、以下の3つの変数を使って重回帰分析を行ったとします 。
- 変数①:店舗面積
- 変数②:従業員数
- 変数③:座席数
これらを独立変数、売上を従属変数として分析した結果、以下のような回帰式が得られたと仮定しましょう 。
y = 0.264x + 0.196z – 0.016p – 0.133
この結果を見ると、変数③(座席数)の係数が「ー(マイナス)」になっています 。
これはつまり、「座席数が増えると売上が減る」ことを意味します 。
一方、この重回帰式のグラフをみると↓こうなってたとします。
このような場合、式とグラフが矛盾していると考えらます。
これこそが、多重共線性が起きているサインなのです
対応①変数同士の相関を確認する
多重共線性への最も基本的な対応は、「変数同士の相関係数をみる」ことです 。
先ほどの例で、説明変数間の相関係数を確認してみると、以下のようになっている可能性があります 。
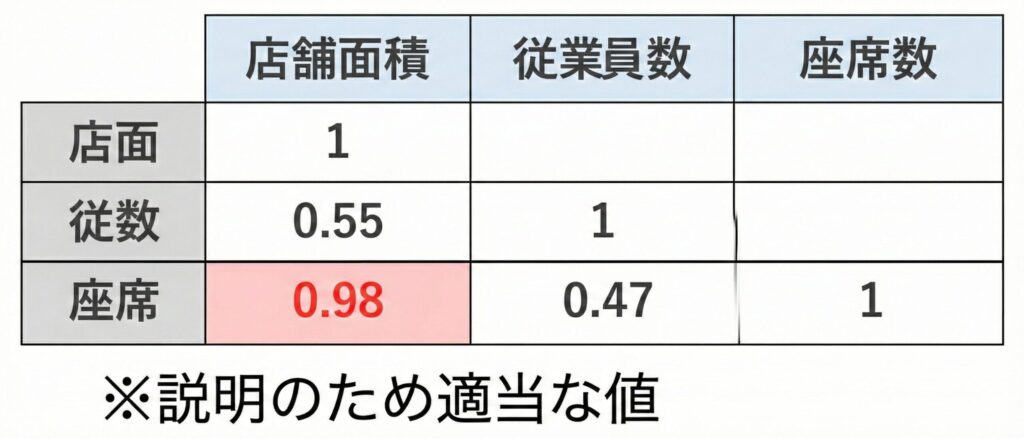
この表を見ると、店舗面積と座席数の相関係数が「0.98」と極めて高くなっています 。
つまり、これが原因で分析が不安定になっていたと考えられます 。
ですので、このような場合は、「店舗面積」または「座席数」のどちらかの変数を除外することで、分析結果を安定させることができるというわけです(^^♪
対応②重相関係数を確認する
ただし、単純な2変数間の相関係数を見るだけでは不十分なケースもあります 。
例えば、以下のような相関表の場合です 。
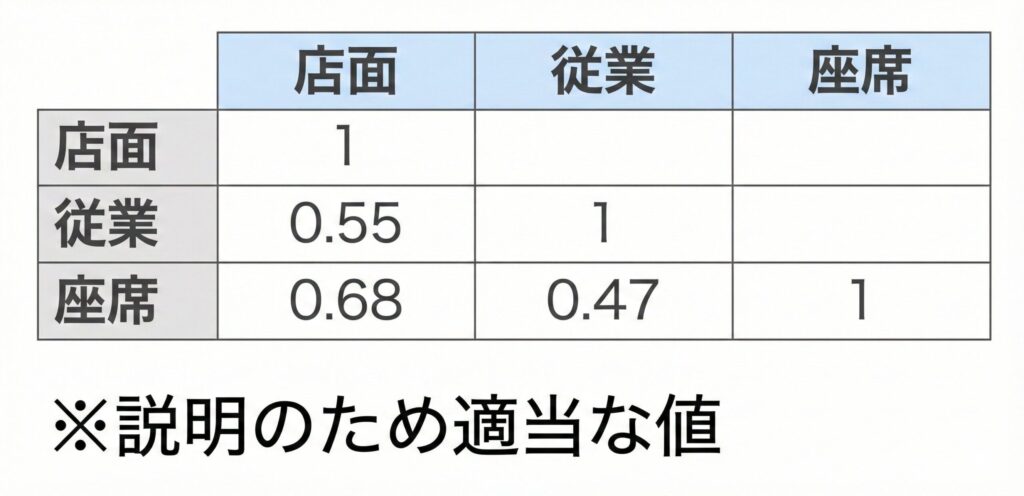
この表では、どの組み合わせも「極端に強い相関」は見当たりません 。
にもかかわらず、多重共線性が疑われる場合には、説明変数同士の「重相関係数」をチェックする必要があります 。
説明変数が3つ以上のデータの多重共線性を検出するためには、2変数間の相関を見るだけでは不十分であり、重相関係数のように「各説明変数と他の説明変数全体との関係」を表す指標を参照する必要がある
(引用:多変量データ解析法 P53. 2段落 3-5行)
重相関係数によるチェック方法
ここでいう重相関係数とは、「ある説明変数を『従属変数』に見立て、他の説明変数を『独立変数』として重回帰分析を行ったときの実測値と予測値の相関」のことです 。
つまり、
- 変数① = 店舗面積
- 変数② = 従業員数
- 変数③ = 座席数
に対して、店舗面積と従業員数を独立変数、 座席数を従属変数として重回帰分析を行い 実測値と予測値の相関係数を求めるというこ と
ちなみに、重回帰分析を行う組み合わせは 以下の3パターンということになります。
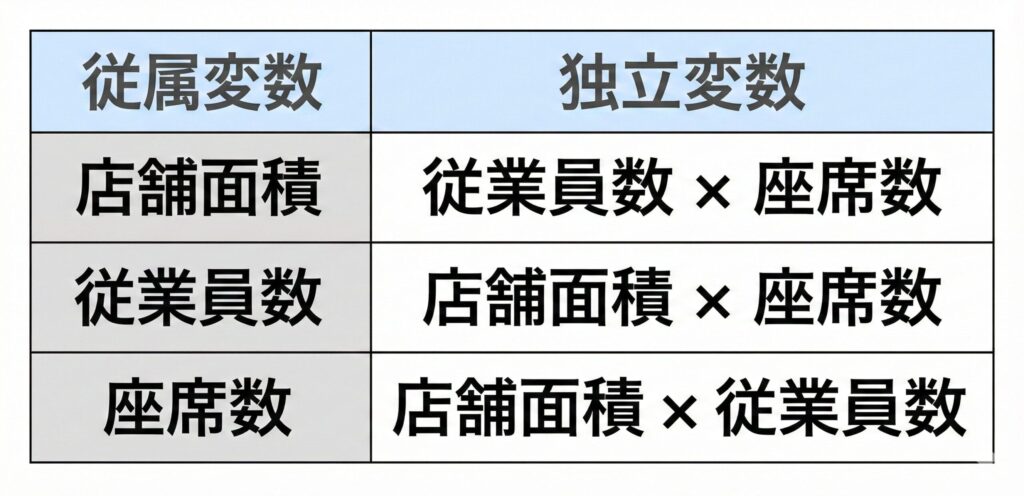
そしてその結果、もし以下のような数値が出たとします…
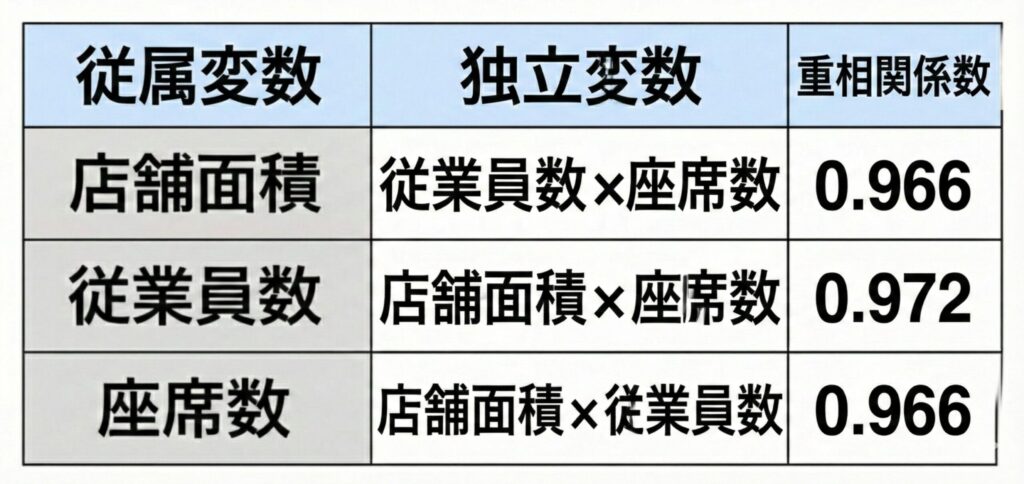
ここからわかるよに、重相関係数をみると、いずれも数値が高くなっています。
この様な場合も、多重共線性(マルチコ)が生じる原因になるのです。
「すなわち、2つの変数間の『1』対『1』の相関は特に高くはないが、重相関係数が示す『1』対『多』の相関は非常に高く、表5.6のデータが多重共線性を持つことがわかる」 (引用:多変量データ解析法、P53、8-10行目)
なので、結局、対応としては、相関係数のときと同じになります。
「多重共線性の問題に対処する方法の1つは、いずれかの説明変数を除くことである」
(引用:多変量データ解析法、P53、3段落、1行目)
まとめ
いかがでしたでしょうか?
多重共線性について少しは理解が深まったでしょうか? 最後に本記事の内容を振り返っておわかれです(^^)/
- 多重共線性とは、説明変数同士に強い相関があり、分析結果が不安定になること
- まずは「相関係数」をチェックして、高すぎる変数を削るのが基本
- 2変数間の相関が低くても、「重相関係数」が高いパターンもあるので要注意!
ということなんですね~ それではまた(^^ゞ
参考
こちらの記事を作成にする上での参考文献です(^ω^)
①多変量解析がわかる
②多変量データ解析法
③例題とExcel演習で学ぶ多変量解析






コメント