この記事は、心理系大学院生や統計を学ぶ方を対象とした学習ページです。
- 重回帰分析の結果が出たけど、どう読み取ればいいかわからない
- 偏回帰係数や重決定係数って何を意味しているの?
- Excelで出力された結果の見方を知りたい
こんな悩みや疑問がある方はご参考ください( ˘ω˘)
今回は、アドインを使って出力した結果👇に基づき情報の読み取りを進めます。
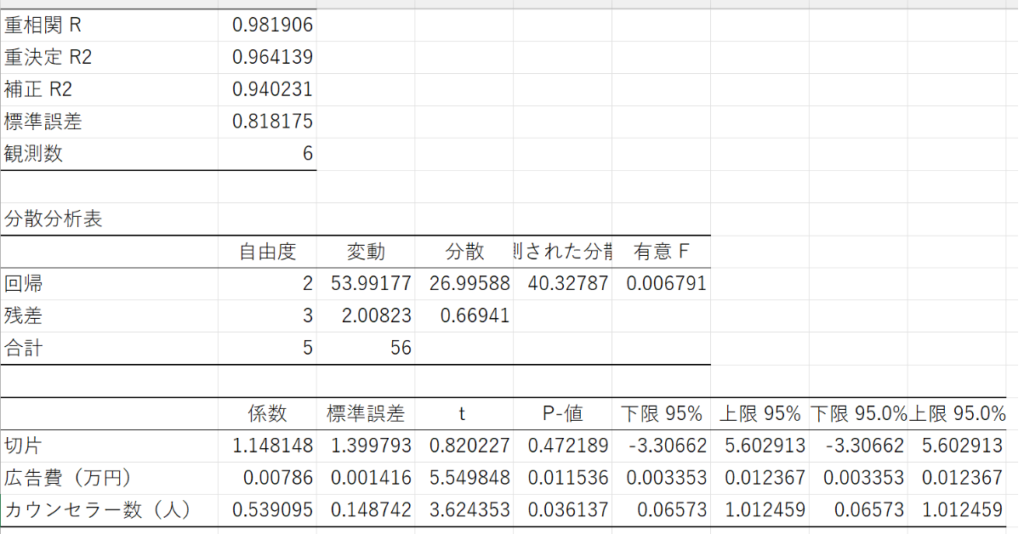
まずは、重回帰式から読み取る
ここから読み取れる重回帰式は次の通りです。
- y = 0.008x + 0.539z + 1.148
これは、以下の赤枠の部分から読み取れます。
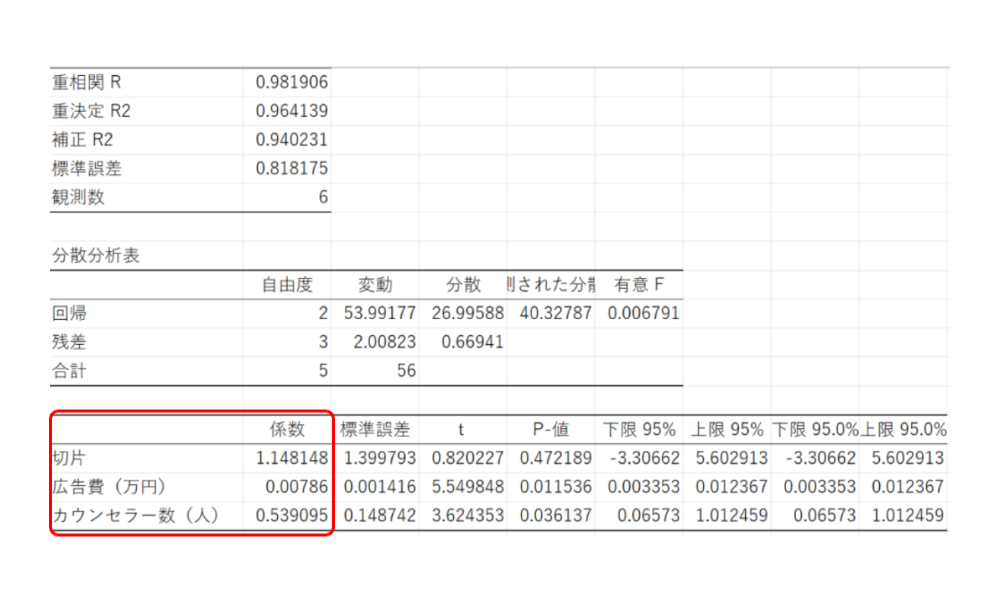
つまり、「係数=偏回帰係数」ということでもあるわけですね。
偏回帰係数の読み取り
次に、👇この式が何を意味するか読み取ります。
- y = 0.008x + 0.539z + 1.148
まず、「0.008x」の部分をみます。
そして、「変数x=広告費」であり、広告費は単位が「万」です。
これは、広告費xが1(1万円)増えると売上yが0.008増えることを意味しています。
つまり、売上(変数y)の単位は「千万」なので、0.008千万 = 8万円増えることを意味しています。
次に、カウンセラー数zは、単位が「人」であるため、1人増えると、売上が0.539(千万)増えることを意味します。
つまり、539万円ということです。
この様な情報を偏回帰係数から読み取ることができます。
※偏回帰係数については解説記事を工事中
注意点:標準解との違い
但し、この重回帰式は、非標準解であるため、変数間で影響力の大きさを比較するためには、標準解を求める必要があります。
標準回帰係数についてのまとめは↓↓こちら
重決定係数の読み取り
次に、重決定係数をみます。
重決定係数は、母集団における重回帰式のあてはまり具合を示す指標で、最大で「1」をとります。
そして、重決定係数は👇これです
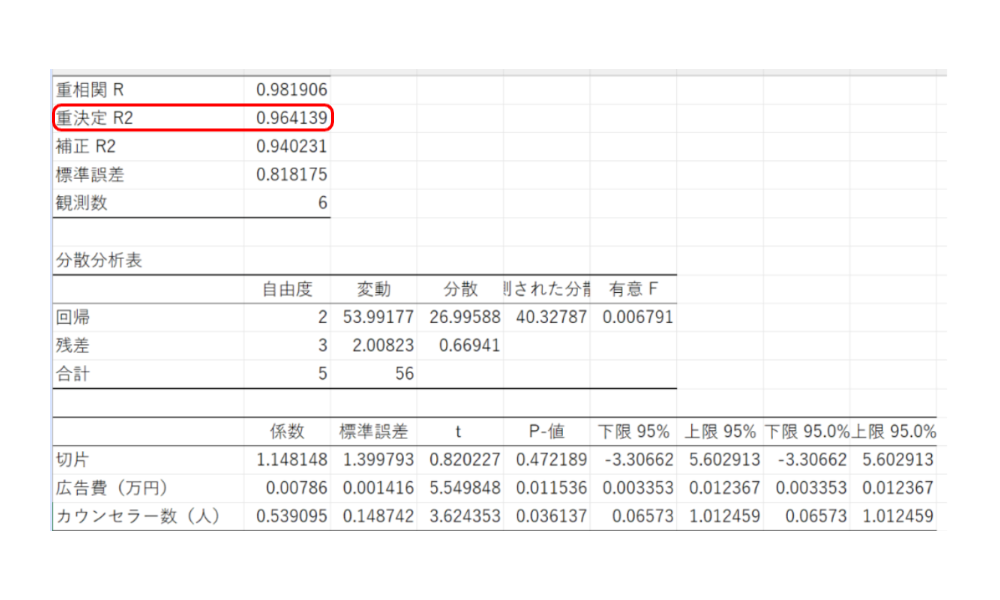
つまり、今回の場合。 R² = 0.964 なので、かなり精度は高いと考えられます。
ただし、変数が少ないため、👇自由度修正済み決定係数もみます。
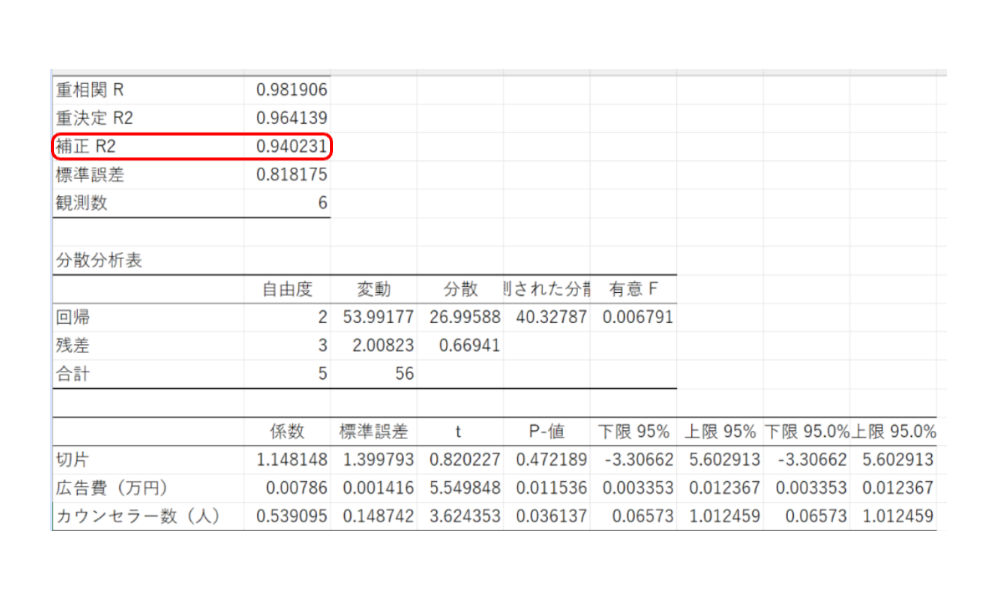
補正R² = 0.940なので、この結果をみても精度は高いと考えられます。
分散分析表をみる
ただし、この結果は、あくまでも、標本としてのデータからの結果でしかありません。
「一部分のサンプルから全体(母集団)のことを調べる場合、決定係数の検定をしなければなりません。
決定係数の検定の仮説は次となります。
- 帰無仮説:決定係数は0である
- 対立仮説:決定係数は0ではない
検定は対立仮説が採択できるかを検討するものです。」
(引用:例題とExcel演習で学ぶ多変量解析、P107.13-18行目)
つまり、ここで求められた決定係数が有効か否かを、通常は吟味する必要があるということです。
そして、その結果を示しているのが↓↓「分散分析表」です。
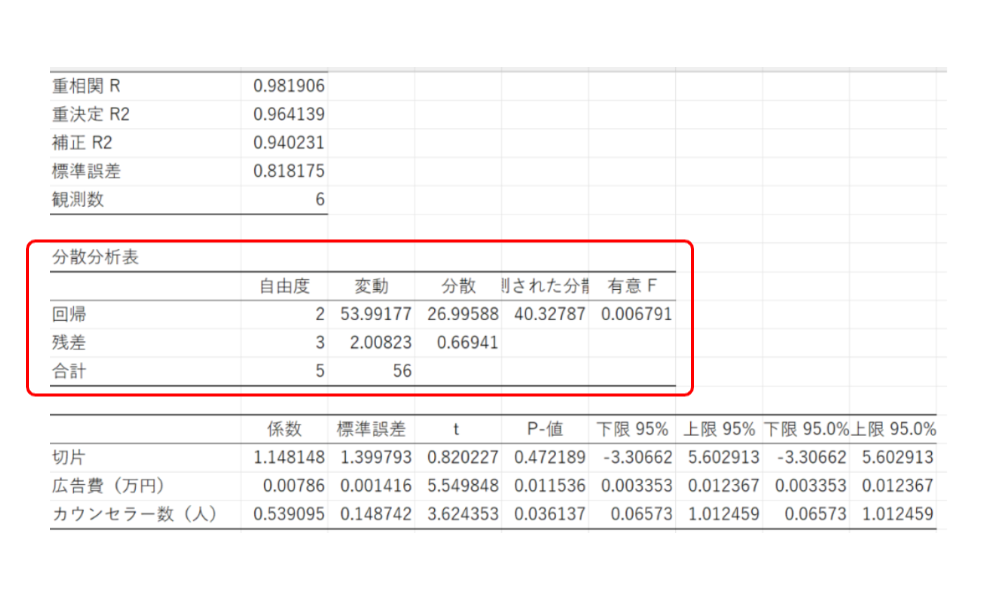
とりあえず、ここでは、「有意F」のみ確認します。
なぜなら、これが有意差を確認する指標だからです。
つまり、「有意F=0.00679」ということは、
「有意F<0.05」なわけですから「有意差あり」ということになるわけです(^^ゞ
回帰式の係数(偏回帰係数)の推定・検定
また、先ほどは飛ばしましたが、同様に偏回帰係数についても母集団に適用可能かどうかを確かめる必要があります。
「における偏回帰係数についての検定は、『母集団偏回帰係数は0(14.16式に示すように)これの一定倍である標準偏回帰係数も0である』という帰無仮説を検証する。この仮説は、『当該説明変数が従属変数に寄与しない』こととして言い換えられる」
(引用:多変量データ解析法P51.15.6..重相関係数の検定と偏回帰係数の区間推定」、4段、1-3行)
つまり、
- 帰無仮説:当該説明変数が従属変数に寄与しない
- 対立仮説:当該説明変数は従属変数に寄与する
ということなので、帰無仮説が棄却される = 対立仮説が採用されることになります。
これは、係数ごとにみる必要があり、P値をみます。
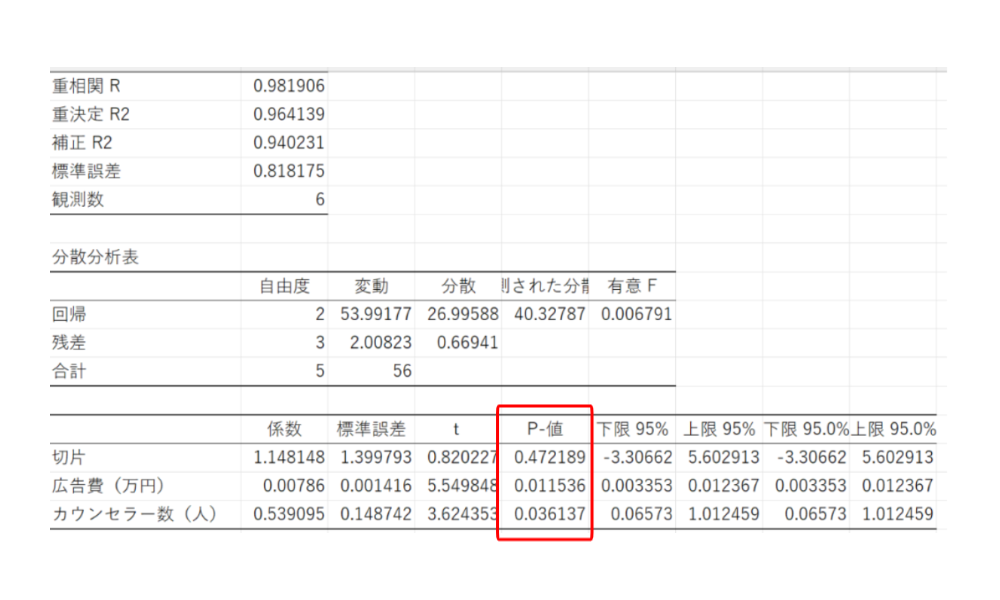
検定の結果が↓↓こちら
- 切片 → 「0.472 > 0.05」で有意差なし
- 広告費 → 「0.012 < 0.05」で有意差あり
- カウンセラー数 → 「0.036 < 0.05」で有意差あり
という結果になります。
回帰係数の区間推定とは?
母集団への適用の可否がわかったら信頼区間も見ておきましょう(=゚ω゚)ノ
これに関しては、別途記事を用意しておきましたのでご参考ください♪
標準誤差もあわせてみる
また、標準誤差もあわせてみるとよいです。
というのも、「標準誤差」=「母集団における係数のデータのバラツキ」なので、これをみることで、サンプルから得られた係数の精度がイメージできるからです。
例えば、以下の表の場合、広告費の標準誤差 = 0.001なので、ズレが非常に小さいであろうとわかります。

また、P値も0.012と非常に小さいため、納得のいくものであります。
一方、カウンセラー数の標準誤差 = 0.148で、それに合わせて、P値も0.036と広告費の場合と比べて大きくなっているので、標準誤差と連動していることがわかります。
また、切片の標準誤差 = 1.399と、他2つの係数に比べ、バラつきが大きいとわかります。
このことからも、唯一、切片の有意差がなかったのも納得できます。
まとめ
いかがでしたでしょうか?
重回帰分析の結果の読み取り方について、少しは理解が深まったでしょうか?
最後に本記事の内容を振り返っておわかれです(^^)/
- 重回帰式は、出力結果の係数から読み取ることができ、各偏回帰係数が変数間の関係を示している
- 重決定係数R²は、重回帰式の精度(あてはまり具合)を示す指標で、1に近いほど精度が高い
- P値を確認することで、各係数が統計的に意味があるかどうか(母集団に適用できるか)を判断
- 標準誤差は、母集団の分散のバラツキを示している。
ということなんですね〜
それではまた(^^ゞ





コメント